Deep Reinforcement Learning for Online Control of Stochastic Partial Differential Equations

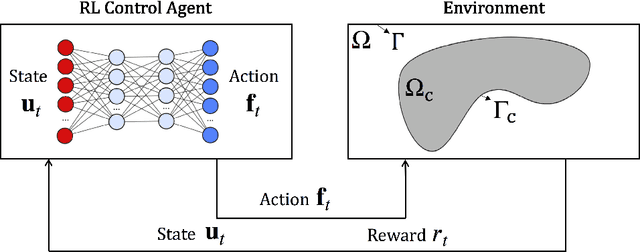
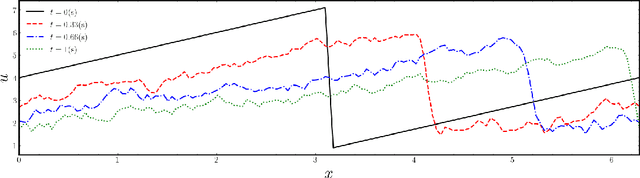
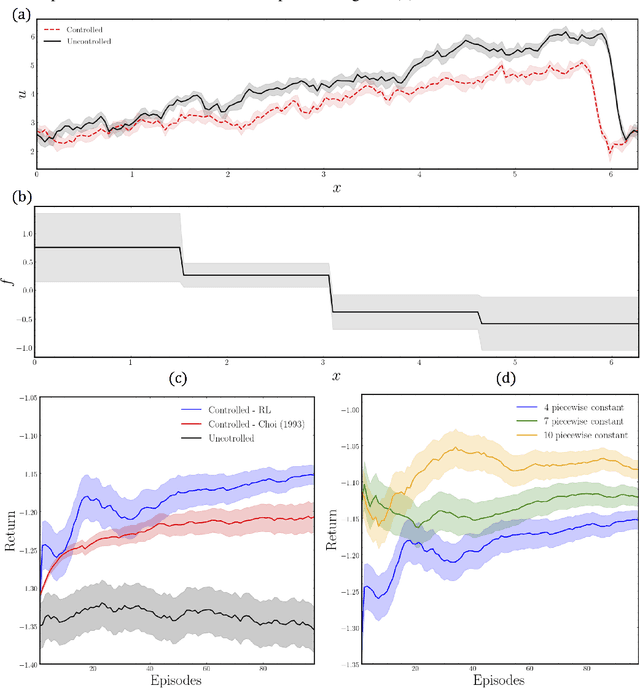
In many areas, such as the physical sciences, life sciences, and finance, control approaches are used to achieve a desired goal in complex dynamical systems governed by differential equations. In this work we formulate the problem of controlling stochastic partial differential equations (SPDE) as a reinforcement learning problem. We present a learning-based, distributed control approach for online control of a system of SPDEs with high dimensional state-action space using deep deterministic policy gradient method. We tested the performance of our method on the problem of controlling the stochastic Burgers' equation, describing a turbulent fluid flow in an infinitely large domain.

A Deep Learning Algorithm for Piecewise Linear Interface Construction (PLIC)

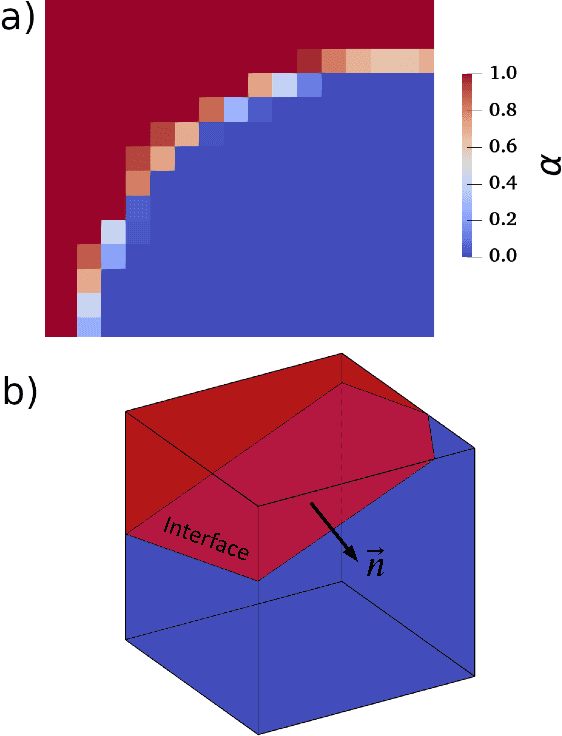
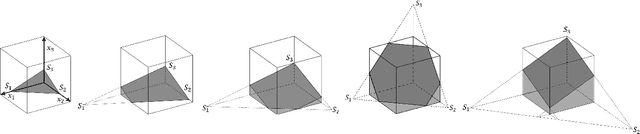
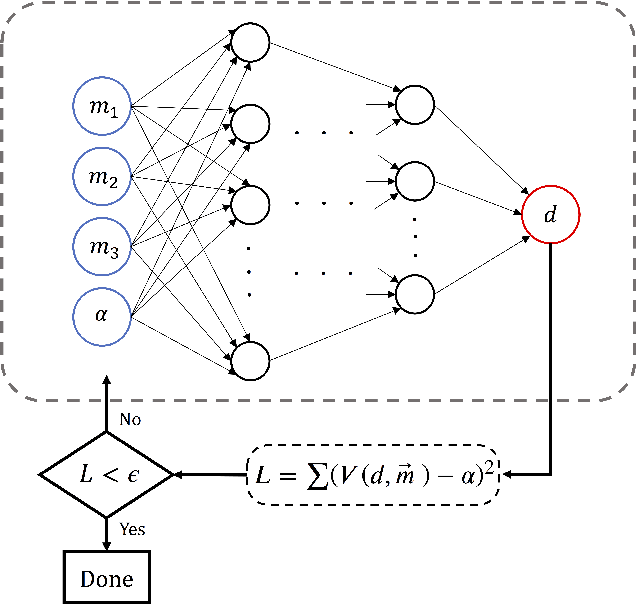
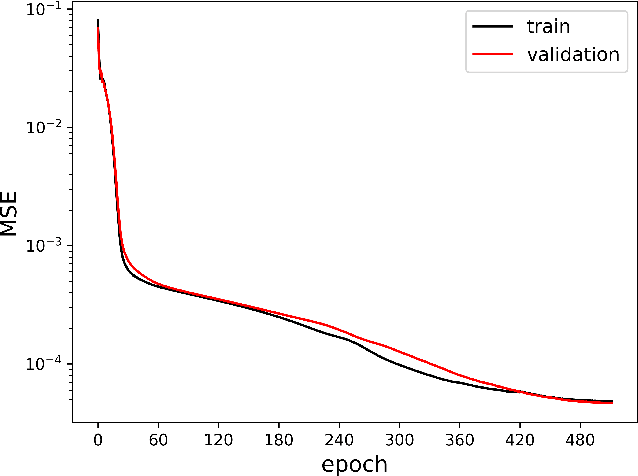
Piecewise Linear Interface Construction (PLIC) is frequently used to geometrically reconstruct fluid interfaces in Computational Fluid Dynamics (CFD) modeling of two-phase flows. PLIC reconstructs interfaces from a scalar field that represents the volume fraction of each phase in each computational cell. Given the volume fraction and interface normal, the location of a linear interface is uniquely defined. For a cubic computational cell (3D), the position of the planar interface is determined by intersecting the cube with a plane, such that the volume of the resulting truncated polyhedron cell is equal to the volume fraction. Yet it is geometrically complex to find the exact position of the plane, and it involves calculations that can be a computational bottleneck of many CFD models. However, while the forward problem of 3D PLIC is challenging, the inverse problem, of finding the volume of the truncated polyhedron cell given a defined plane, is simple. In this work, we propose a deep learning model for the solution to the forward problem of PLIC by only making use of its inverse problem. The proposed model is up to several orders of magnitude faster than traditional schemes, which significantly reduces the computational bottleneck of PLIC in CFD simulations.