Mohammadmehdi Ataei
MechaFormer: Sequence Learning for Kinematic Mechanism Design Automation
Aug 12, 2025Abstract:Designing mechanical mechanisms to trace specific paths is a classic yet notoriously difficult engineering problem, characterized by a vast and complex search space of discrete topologies and continuous parameters. We introduce MechaFormer, a Transformer-based model that tackles this challenge by treating mechanism design as a conditional sequence generation task. Our model learns to translate a target curve into a domain-specific language (DSL) string, simultaneously determining the mechanism's topology and geometric parameters in a single, unified process. MechaFormer significantly outperforms existing baselines, achieving state-of-the-art path-matching accuracy and generating a wide diversity of novel and valid designs. We demonstrate a suite of sampling strategies that can dramatically improve solution quality and offer designers valuable flexibility. Furthermore, we show that the high-quality outputs from MechaFormer serve as excellent starting points for traditional optimizers, creating a hybrid approach that finds superior solutions with remarkable efficiency.
RECALL-MM: A Multimodal Dataset of Consumer Product Recalls for Risk Analysis using Computational Methods and Large Language Models
Mar 29, 2025

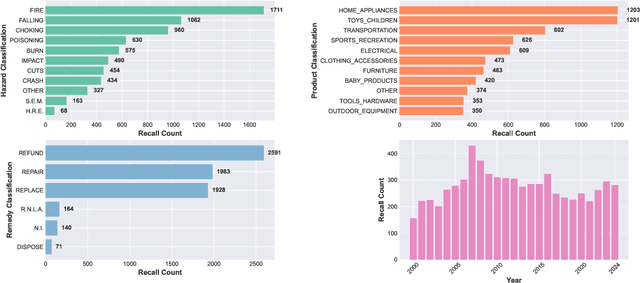
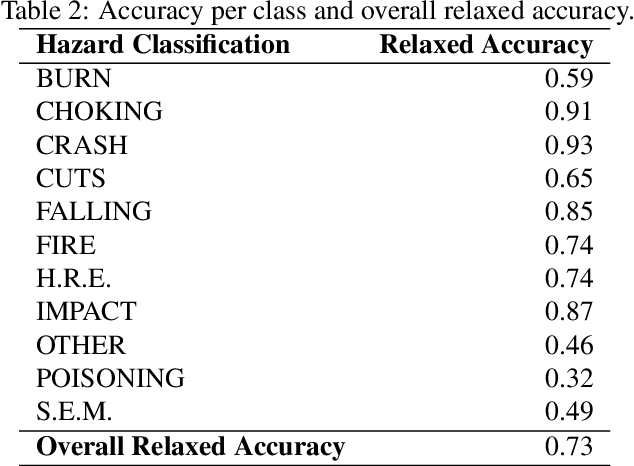
Abstract:Product recalls provide valuable insights into potential risks and hazards within the engineering design process, yet their full potential remains underutilized. In this study, we curate data from the United States Consumer Product Safety Commission (CPSC) recalls database to develop a multimodal dataset, RECALL-MM, that informs data-driven risk assessment using historical information, and augment it using generative methods. Patterns in the dataset highlight specific areas where improved safety measures could have significant impact. We extend our analysis by demonstrating interactive clustering maps that embed all recalls into a shared latent space based on recall descriptions and product names. Leveraging these data-driven tools, we explore three case studies to demonstrate the dataset's utility in identifying product risks and guiding safer design decisions. The first two case studies illustrate how designers can visualize patterns across recalled products and situate new product ideas within the broader recall landscape to proactively anticipate hazards. In the third case study, we extend our approach by employing a large language model (LLM) to predict potential hazards based solely on product images. This demonstrates the model's ability to leverage visual context to identify risk factors, revealing strong alignment with historical recall data across many hazard categories. However, the analysis also highlights areas where hazard prediction remains challenging, underscoring the importance of risk awareness throughout the design process. Collectively, this work aims to bridge the gap between historical recall data and future product safety, presenting a scalable, data-driven approach to safer engineering design.
e-SimFT: Alignment of Generative Models with Simulation Feedback for Pareto-Front Design Exploration
Feb 04, 2025



Abstract:Deep generative models have recently shown success in solving complex engineering design problems where models predict solutions that address the design requirements specified as input. However, there remains a challenge in aligning such models for effective design exploration. For many design problems, finding a solution that meets all the requirements is infeasible. In such a case, engineers prefer to obtain a set of Pareto optimal solutions with respect to those requirements, but uniform sampling of generative models may not yield a useful Pareto front. To address this gap, we introduce a new framework for Pareto-front design exploration with simulation fine-tuned generative models. First, the framework adopts preference alignment methods developed for Large Language Models (LLMs) and showcases the first application in fine-tuning a generative model for engineering design. The important distinction here is that we use a simulator instead of humans to provide accurate and scalable feedback. Next, we propose epsilon-sampling, inspired by the epsilon-constraint method used for Pareto-front generation with classical optimization algorithms, to construct a high-quality Pareto front with the fine-tuned models. Our framework, named e-SimFT, is shown to produce better-quality Pareto fronts than existing multi-objective alignment methods.
mPOLICE: Provable Enforcement of Multi-Region Affine Constraints in Deep Neural Networks
Feb 04, 2025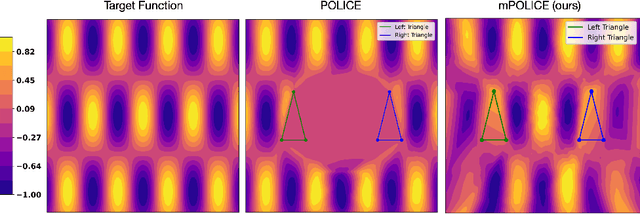


Abstract:Deep neural networks are increasingly employed in fields such as climate modeling, robotics, and industrial control, where strict output constraints must be upheld. Although prior methods like the POLICE algorithm can enforce affine constraints in a single convex region by adjusting network parameters, they struggle with multiple disjoint regions, often leading to conflicts or unintended affine extensions. We present mPOLICE, a new method that extends POLICE to handle constraints imposed on multiple regions. mPOLICE assigns a distinct activation pattern to each constrained region, preserving exact affine behavior locally while avoiding overreach into other parts of the input domain. We formulate a layer-wise optimization problem that adjusts both the weights and biases to assign unique activation patterns to each convex region, ensuring that constraints are met without conflicts, while maintaining the continuity and smoothness of the learned function. Our experiments show the enforcement of multi-region constraints for multiple scenarios, including regression and classification, function approximation, and non-convex regions through approximation. Notably, mPOLICE adds zero inference overhead and minimal training overhead.
Synthetic Vision: Training Vision-Language Models to Understand Physics
Dec 11, 2024



Abstract:Physical reasoning, which involves the interpretation, understanding, and prediction of object behavior in dynamic environments, remains a significant challenge for current Vision-Language Models (VLMs). In this work, we propose two methods to enhance VLMs' physical reasoning capabilities using simulated data. First, we fine-tune a pre-trained VLM using question-answer (QA) pairs generated from simulations relevant to physical reasoning tasks. Second, we introduce Physics Context Builders (PCBs), specialized VLMs fine-tuned to create scene descriptions enriched with physical properties and processes. During physical reasoning tasks, these PCBs can be leveraged as context to assist a Large Language Model (LLM) to improve its performance. We evaluate both of our approaches using multiple benchmarks, including a new stability detection QA dataset called Falling Tower, which includes both simulated and real-world scenes, and CLEVRER. We demonstrate that a small QA fine-tuned VLM can significantly outperform larger state-of-the-art foundational models. We also show that integrating PCBs boosts the performance of foundational LLMs on physical reasoning tasks. Using the real-world scenes from the Falling Tower dataset, we also validate the robustness of both approaches in Sim2Real transfer. Our results highlight the utility that simulated data can have in the creation of learning systems capable of advanced physical reasoning.
Deep Generative Model for Mechanical System Configuration Design
Sep 09, 2024



Abstract:Generative AI has made remarkable progress in addressing various design challenges. One prominent area where generative AI could bring significant value is in engineering design. In particular, selecting an optimal set of components and their interfaces to create a mechanical system that meets design requirements is one of the most challenging and time-consuming tasks for engineers. This configuration design task is inherently challenging due to its categorical nature, multiple design requirements a solution must satisfy, and the reliance on physics simulations for evaluating potential solutions. These characteristics entail solving a combinatorial optimization problem with multiple constraints involving black-box functions. To address this challenge, we propose a deep generative model to predict the optimal combination of components and interfaces for a given design problem. To demonstrate our approach, we solve a gear train synthesis problem by first creating a synthetic dataset using a grammar, a parts catalogue, and a physics simulator. We then train a Transformer using this dataset, named GearFormer, which can not only generate quality solutions on its own, but also augment search methods such as an evolutionary algorithm and Monte Carlo tree search. We show that GearFormer outperforms such search methods on their own in terms of satisfying the specified design requirements with orders of magnitude faster generation time. Additionally, we showcase the benefit of hybrid methods that leverage both GearFormer and search methods, which further improve the quality of the solutions.
Reduced-order modeling of unsteady fluid flow using neural network ensembles
Feb 08, 2024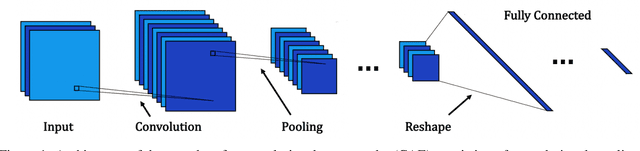
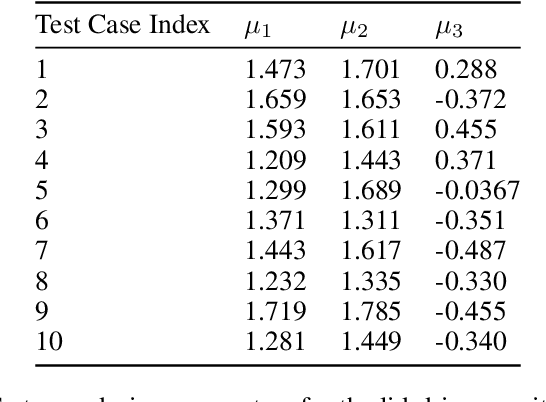
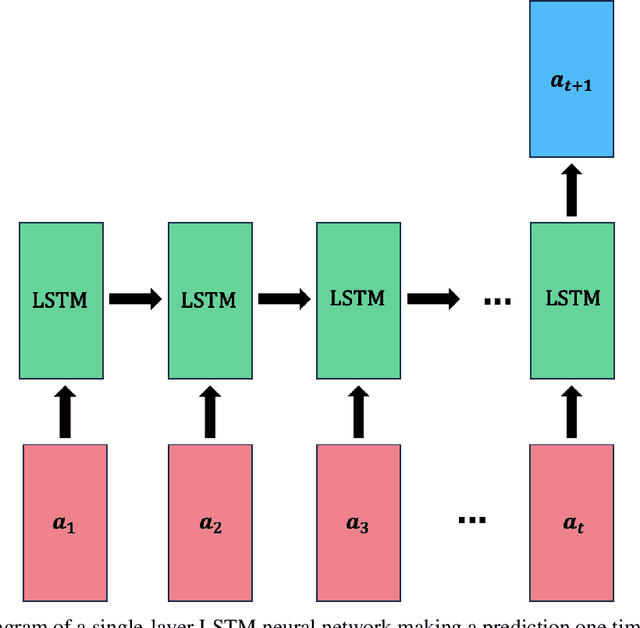
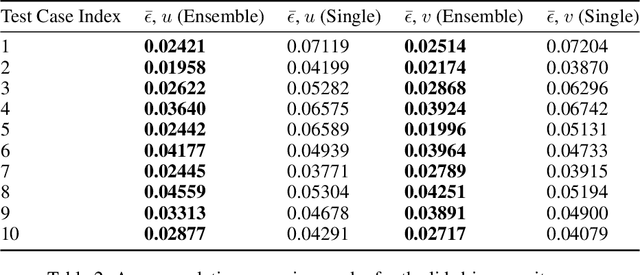
Abstract:The use of deep learning has become increasingly popular in reduced-order models (ROMs) to obtain low-dimensional representations of full-order models. Convolutional autoencoders (CAEs) are often used to this end as they are adept at handling data that are spatially distributed, including solutions to partial differential equations. When applied to unsteady physics problems, ROMs also require a model for time-series prediction of the low-dimensional latent variables. Long short-term memory (LSTM) networks, a type of recurrent neural network useful for modeling sequential data, are frequently employed in data-driven ROMs for autoregressive time-series prediction. When making predictions at unseen design points over long time horizons, error propagation is a frequently encountered issue, where errors made early on can compound over time and lead to large inaccuracies. In this work, we propose using bagging, a commonly used ensemble learning technique, to develop a fully data-driven ROM framework referred to as the CAE-eLSTM ROM that uses CAEs for spatial reconstruction of the full-order model and LSTM ensembles for time-series prediction. When applied to two unsteady fluid dynamics problems, our results show that the presented framework effectively reduces error propagation and leads to more accurate time-series prediction of latent variables at unseen points.
XLB: Distributed Multi-GPU Lattice Boltzmann Simulation Framework for Differentiable Scientific Machine Learning
Nov 27, 2023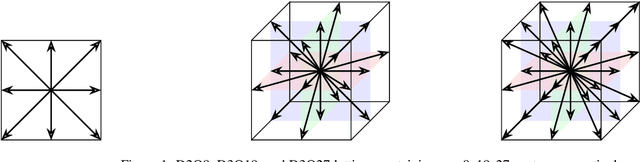

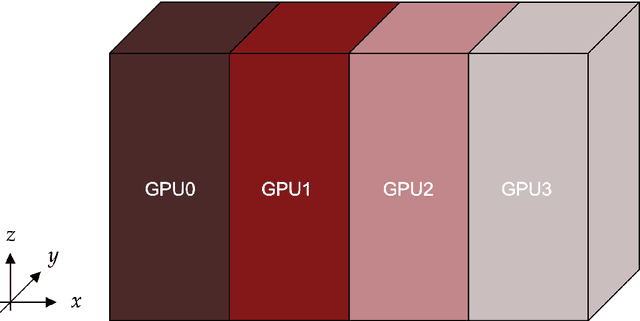
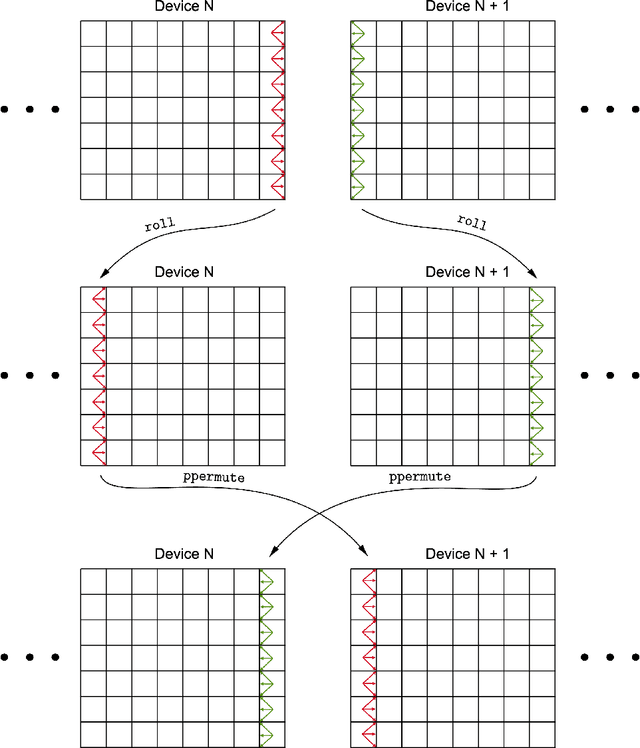
Abstract:The lattice Boltzmann method (LBM) has emerged as a prominent technique for solving fluid dynamics problems due to its algorithmic potential for computational scalability. We introduce XLB framework, a Python-based differentiable LBM library which harnesses the capabilities of the JAX framework. The architecture of XLB is predicated upon ensuring accessibility, extensibility, and computational performance, enabling scaling effectively across CPU, multi-GPU, and distributed multi-GPU systems. The framework can be readily augmented with novel boundary conditions, collision models, or simulation capabilities. XLB offers the unique advantage of integration with JAX's extensive machine learning echosystem, and the ability to utilize automatic differentiation for tackling physics-based machine learning, optimization, and inverse problems. XLB has been successfully scaled to handle simulations with billions of cells, achieving giga-scale lattice updates per second. XLB is released under the permissive Apache-2.0 license and is available on GitHub at https://github.com/Autodesk/XLB.
A Deep Learning Algorithm for Piecewise Linear Interface Construction (PLIC)
Jul 27, 2021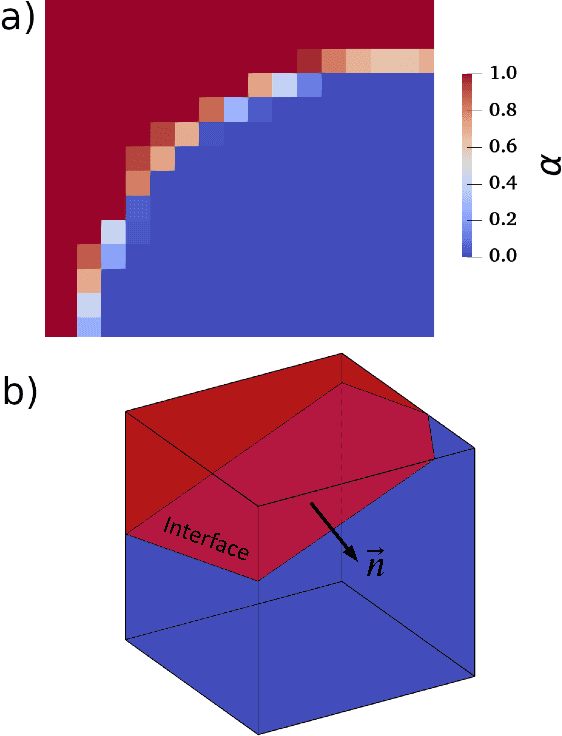
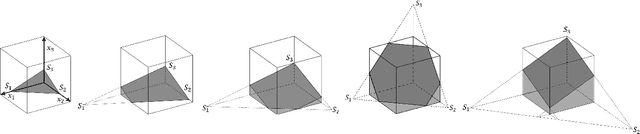
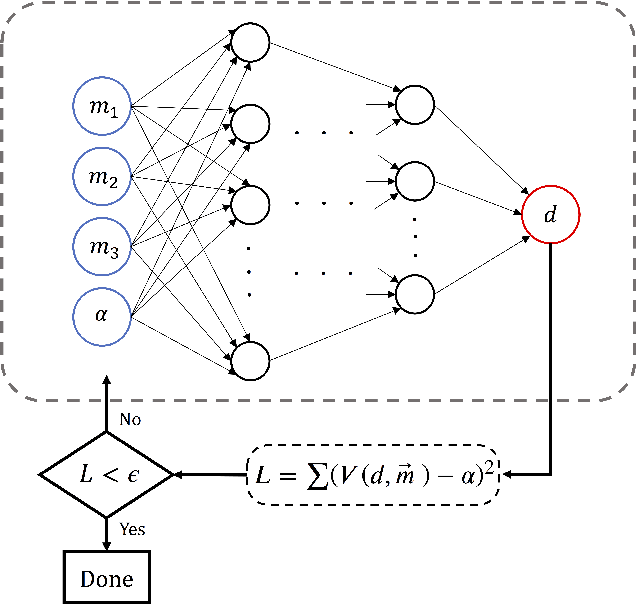
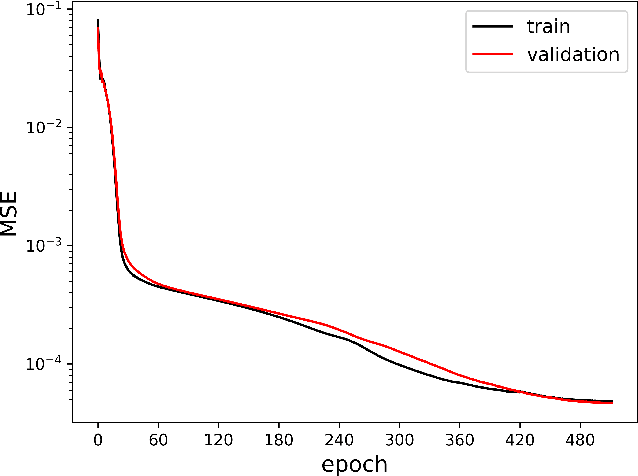
Abstract:Piecewise Linear Interface Construction (PLIC) is frequently used to geometrically reconstruct fluid interfaces in Computational Fluid Dynamics (CFD) modeling of two-phase flows. PLIC reconstructs interfaces from a scalar field that represents the volume fraction of each phase in each computational cell. Given the volume fraction and interface normal, the location of a linear interface is uniquely defined. For a cubic computational cell (3D), the position of the planar interface is determined by intersecting the cube with a plane, such that the volume of the resulting truncated polyhedron cell is equal to the volume fraction. Yet it is geometrically complex to find the exact position of the plane, and it involves calculations that can be a computational bottleneck of many CFD models. However, while the forward problem of 3D PLIC is challenging, the inverse problem, of finding the volume of the truncated polyhedron cell given a defined plane, is simple. In this work, we propose a deep learning model for the solution to the forward problem of PLIC by only making use of its inverse problem. The proposed model is up to several orders of magnitude faster than traditional schemes, which significantly reduces the computational bottleneck of PLIC in CFD simulations.
NPLIC: A Machine Learning Approach to Piecewise Linear Interface Construction
Jun 26, 2020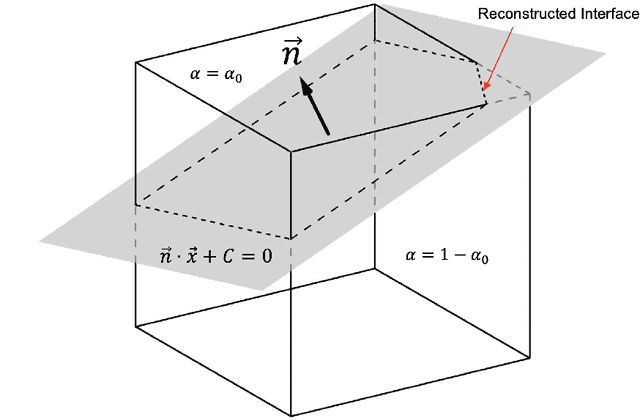
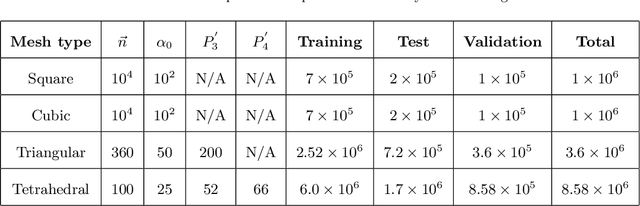
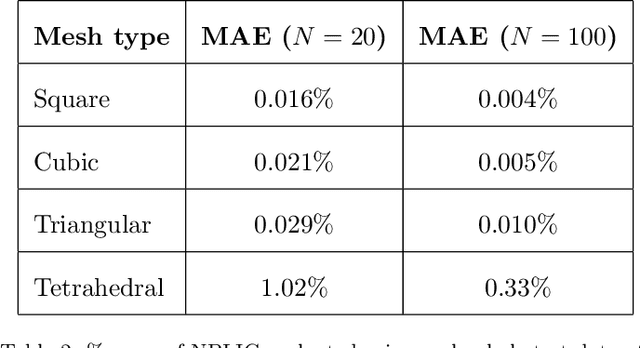
Abstract:Volume of fluid (VOF) methods are extensively used to track fluid interfaces in numerical simulations, and many VOF algorithms require that the interface be reconstructed geometrically. For this purpose, the Piecewise Linear Interface Construction (PLIC) technique is most frequently used, which for reasons of geometric complexity can be slow and difficult to implement. Here, we propose an alternative neural network-based method called NPLIC to perform PLIC calculations. The model is trained on a large synthetic dataset of PLIC solutions for square, cubic, triangular, and tetrahedral meshes. We show that this data-driven approach results in accurate calculations at a fraction of the usual computational cost.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge