Kevin Maki
Reduced-order modeling of unsteady fluid flow using neural network ensembles
Feb 08, 2024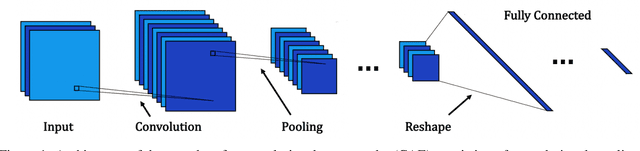
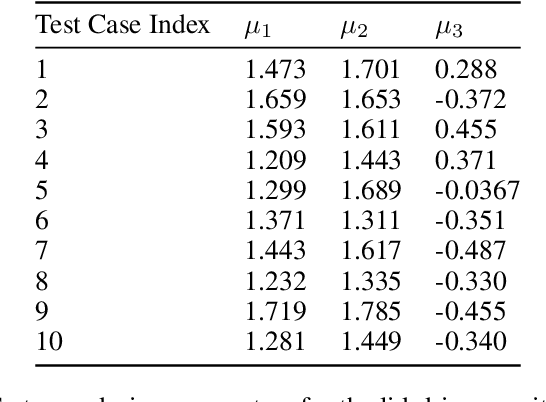
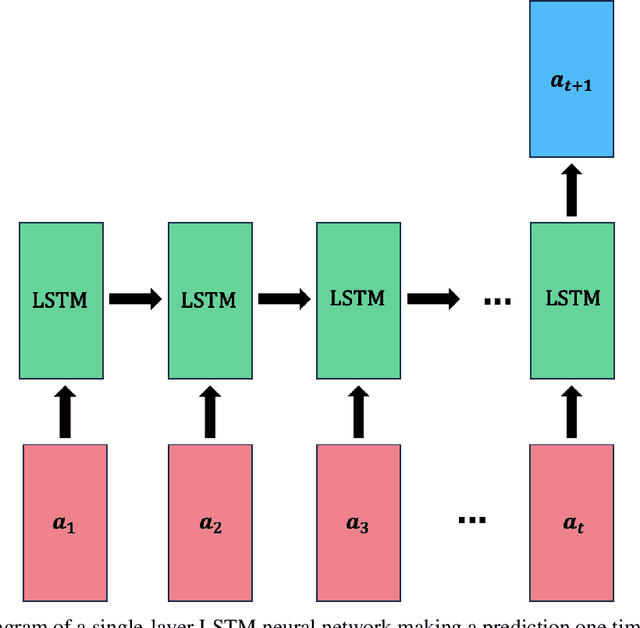
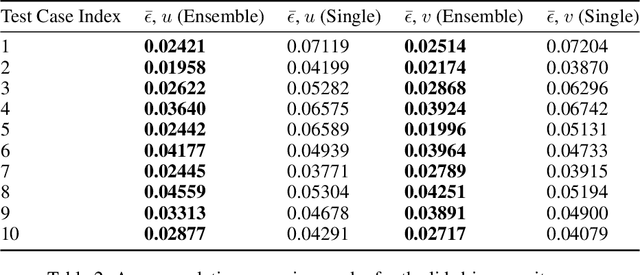
Abstract:The use of deep learning has become increasingly popular in reduced-order models (ROMs) to obtain low-dimensional representations of full-order models. Convolutional autoencoders (CAEs) are often used to this end as they are adept at handling data that are spatially distributed, including solutions to partial differential equations. When applied to unsteady physics problems, ROMs also require a model for time-series prediction of the low-dimensional latent variables. Long short-term memory (LSTM) networks, a type of recurrent neural network useful for modeling sequential data, are frequently employed in data-driven ROMs for autoregressive time-series prediction. When making predictions at unseen design points over long time horizons, error propagation is a frequently encountered issue, where errors made early on can compound over time and lead to large inaccuracies. In this work, we propose using bagging, a commonly used ensemble learning technique, to develop a fully data-driven ROM framework referred to as the CAE-eLSTM ROM that uses CAEs for spatial reconstruction of the full-order model and LSTM ensembles for time-series prediction. When applied to two unsteady fluid dynamics problems, our results show that the presented framework effectively reduces error propagation and leads to more accurate time-series prediction of latent variables at unseen points.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge