LoRA-Drop: Temporal LoRA Decoding for Efficient LLM Inference

Autoregressive large language models (LLMs) are bottlenecked by sequential decoding, where each new token typically requires executing all transformer layers. Existing dynamic-depth and layer-skipping methods reduce this cost, but often rely on auxiliary routing mechanisms or incur accuracy degradation when bypassed layers are left uncompensated. We present \textbf{LoRA-Drop}, a plug-and-play inference framework that accelerates decoding by applying a \emph{temporal compute schedule} to a fixed subset of intermediate layers: on most decoding steps, selected layers reuse the previous-token hidden state and apply a low-rank LoRA correction, while periodic \emph{refresh} steps execute the full model to prevent drift. LoRA-Drop requires no routing network, is compatible with standard KV caching, and can reduce KV-cache footprint by skipping KV updates in droppable layers during LoRA steps and refreshing periodically. Across \textbf{LLaMA2-7B}, \textbf{LLaMA3-8B}, \textbf{Qwen2.5-7B}, and \textbf{Qwen2.5-14B}, LoRA-Drop achieves up to \textbf{2.6$\times$ faster decoding} and \textbf{45--55\% KV-cache reduction} while staying within \textbf{0.5 percentage points (pp)} of baseline accuracy. Evaluations on reasoning (GSM8K, MATH, BBH), code generation (HumanEval, MBPP), and long-context/multilingual benchmarks (LongBench, XNLI, XCOPA) identify a consistent \emph{safe zone} of scheduling configurations that preserves quality while delivering substantial efficiency gains, providing a simple path toward adaptive-capacity inference in LLMs. Codes are available at https://github.com/hosseinbv/LoRA-Drop.git.

NPLIC: A Machine Learning Approach to Piecewise Linear Interface Construction

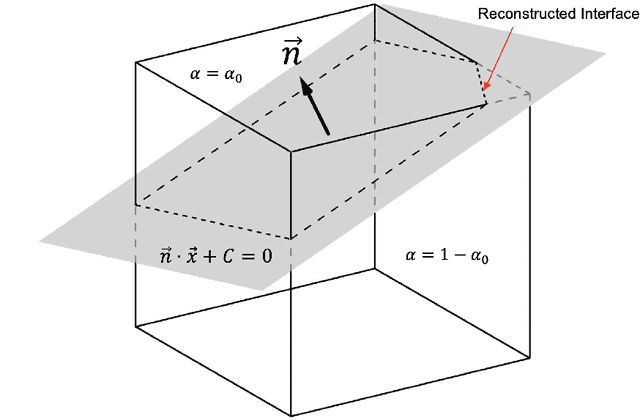
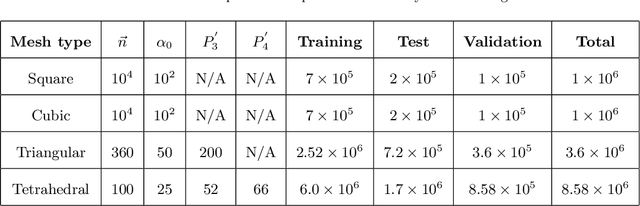
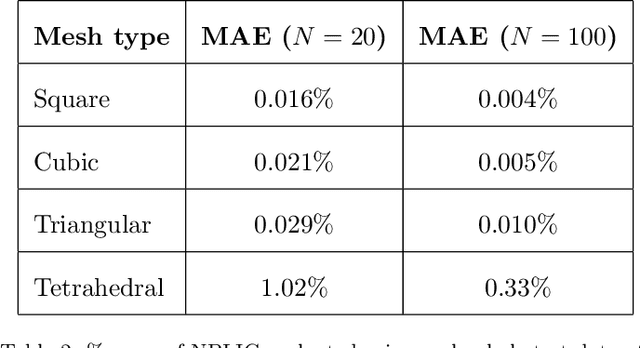
Volume of fluid (VOF) methods are extensively used to track fluid interfaces in numerical simulations, and many VOF algorithms require that the interface be reconstructed geometrically. For this purpose, the Piecewise Linear Interface Construction (PLIC) technique is most frequently used, which for reasons of geometric complexity can be slow and difficult to implement. Here, we propose an alternative neural network-based method called NPLIC to perform PLIC calculations. The model is trained on a large synthetic dataset of PLIC solutions for square, cubic, triangular, and tetrahedral meshes. We show that this data-driven approach results in accurate calculations at a fraction of the usual computational cost.