Physics-based simulation ontology: an ontology to support modelling and reuse of data for physics-based simulation

The current work presents an ontology developed for physics-based simulation in engineering design, called Physics-based Simulation Ontology (PSO). The purpose of the ontology is to assist in modelling the physical phenomenon of interest in a veridical manner, while capturing the necessary and reusable information for physics-based simulation solvers. The development involved extending an existing upper ontology, Basic Formal Ontology (BFO), to define lower-level terms of PSO. PSO has two parts: PSO-Physics, which consists of terms and relations used to model physical phenomena based on the perspective of classical mechanics involving partial differential equations, and PSO-Sim, which consists of terms used to represent the information artefacts that are about the physical phenomena modelled with PSO-Physics. The former terms are used to model the physical phenomenon of interest independent of solver-specific interpretations, which can be reused across different solvers, while the latter terms are used to instantiate solver-specific input data. A case study involving two simulation solvers was conducted to demonstrate this capability of PSO. Discussion around the benefits and limitations of using BFO for the current work is also provided, which should be valuable for any future work that extends an existing upper ontology to develop ontologies for engineering applications.

Configuration Design of Mechanical Assemblies using an Estimation of Distribution Algorithm and Constraint Programming

A configuration design problem in mechanical engineering involves finding an optimal assembly of components and joints that realizes some desired performance criteria. Such a problem is a discrete, constrained, and black-box optimization problem. A novel method is developed to solve the problem by applying Bivariate Marginal Distribution Algorithm (BMDA) and constraint programming (CP). BMDA is a type of Estimation of Distribution Algorithm (EDA) that exploits the dependency knowledge learned between design variables without requiring too many fitness evaluations, which tend to be expensive for the current application. BMDA is extended with adaptive chi-square testing to identify dependencies and Gibbs sampling to generate new solutions. Also, repair operations based on CP are used to deal with infeasible solutions found during search. The method is applied to a vehicle suspension design problem and is found to be more effective in converging to good solutions than a genetic algorithm and other EDAs. These contributions are significant steps towards solving the difficult problem of configuration design in mechanical engineering with evolutionary computation.

mPOLICE: Provable Enforcement of Multi-Region Affine Constraints in Deep Neural Networks

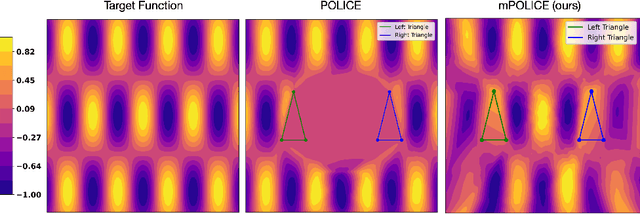
Deep neural networks are increasingly employed in fields such as climate modeling, robotics, and industrial control, where strict output constraints must be upheld. Although prior methods like the POLICE algorithm can enforce affine constraints in a single convex region by adjusting network parameters, they struggle with multiple disjoint regions, often leading to conflicts or unintended affine extensions. We present mPOLICE, a new method that extends POLICE to handle constraints imposed on multiple regions. mPOLICE assigns a distinct activation pattern to each constrained region, preserving exact affine behavior locally while avoiding overreach into other parts of the input domain. We formulate a layer-wise optimization problem that adjusts both the weights and biases to assign unique activation patterns to each convex region, ensuring that constraints are met without conflicts, while maintaining the continuity and smoothness of the learned function. Our experiments show the enforcement of multi-region constraints for multiple scenarios, including regression and classification, function approximation, and non-convex regions through approximation. Notably, mPOLICE adds zero inference overhead and minimal training overhead.

Advancing Fluid-Based Thermal Management Systems Design: Leveraging Graph Neural Networks for Graph Regression and Efficient Enumeration Reduction

In this research, we developed a graph-based framework to represent various aspects of optimal thermal management system design, with the aim of rapidly and efficiently identifying optimal design candidates. Initially, the graph-based framework is utilized to generate diverse thermal management system architectures. The dynamics of these system architectures are modeled under various loading conditions, and an open-loop optimal controller is employed to determine each system's optimal performance. These modeled cases constitute the dataset, with the corresponding optimal performance values serving as the labels for the data. In the subsequent step, a Graph Neural Network (GNN) model is trained on 30% of the labeled data to predict the systems' performance, effectively addressing a regression problem. Utilizing this trained model, we estimate the performance values for the remaining 70% of the data, which serves as the test set. In the third step, the predicted performance values are employed to rank the test data, facilitating prioritized evaluation of the design scenarios. Specifically, a small subset of the test data with the highest estimated ranks undergoes evaluation via the open-loop optimal control solver. This targeted approach concentrates on evaluating higher-ranked designs identified by the GNN, replacing the exhaustive search (enumeration-based) of all design cases. The results demonstrate a significant average reduction of over 92% in the number of system dynamic modeling and optimal control analyses required to identify optimal design scenarios.