The Complexity of Learning Acyclic Conditional Preference Networks
Paper and Code
Aug 25, 2018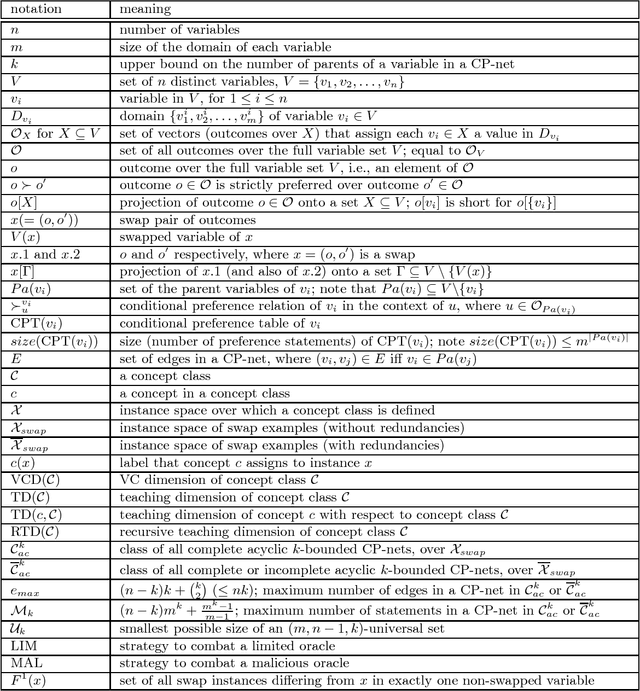



Learning of user preferences, as represented by, for example, Conditional Preference Networks (CP-nets), has become a core issue in AI research. Recent studies investigate learning of CP-nets from randomly chosen examples or from membership and equivalence queries. To assess the optimality of learning algorithms as well as to better understand the combinatorial structure of classes of CP-nets, it is helpful to calculate certain learning-theoretic information complexity parameters. This article focuses on the frequently studied case of learning from so-called swap examples, which express preferences among objects that differ in only one attribute. It presents bounds on or exact values of some well-studied information complexity parameters, namely the VC dimension, the teaching dimension, and the recursive teaching dimension, for classes of acyclic CP-nets. We further provide algorithms that learn tree-structured and general acyclic CP-nets from membership queries. Using our results on complexity parameters, we assess the optimality of our algorithms as well as that of another query learning algorithm for acyclic CP-nets presented in the literature. Our algorithms are near-optimal, and can, under certain assumptions, be adapted to the case when the membership oracle is faulty.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge