Robert C. Holte
Rectangle Search: An Anytime Beam Search (Extended Version)
Dec 19, 2023Abstract:Anytime heuristic search algorithms try to find a (potentially suboptimal) solution as quickly as possible and then work to find better and better solutions until an optimal solution is obtained or time is exhausted. The most widely-known anytime search algorithms are based on best-first search. In this paper, we propose a new algorithm, rectangle search, that is instead based on beam search, a variant of breadth-first search. It repeatedly explores alternatives at all depth levels and is thus best-suited to problems featuring deep local minima. Experiments using a variety of popular search benchmarks suggest that rectangle search is competitive with fixed-width beam search and often performs better than the previous best anytime search algorithms.
Beam Search: Faster and Monotonic
Apr 06, 2022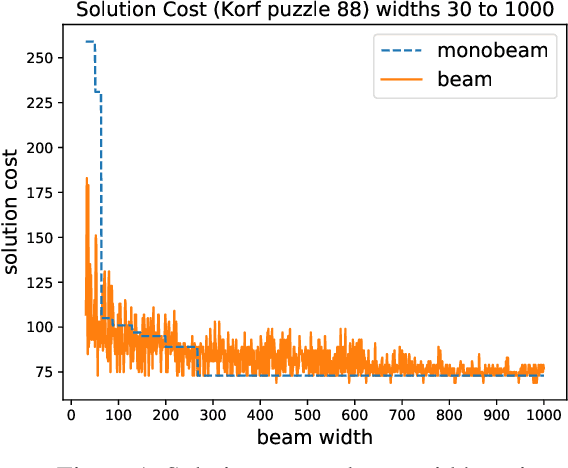

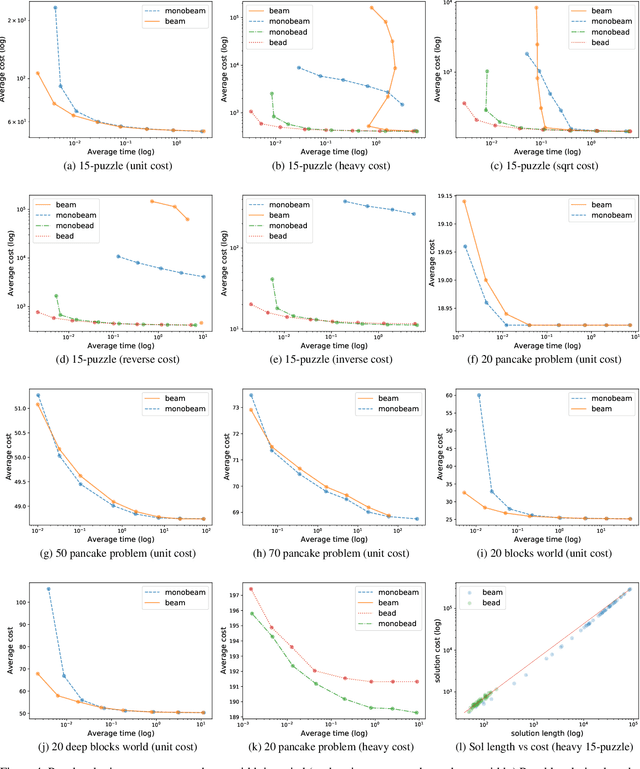
Abstract:Beam search is a popular satisficing approach to heuristic search problems that allows one to trade increased computation time for lower solution cost by increasing the beam width parameter. We make two contributions to the study of beam search. First, we show how to make beam search monotonic; that is, we provide a new variant that guarantees non-increasing solution cost as the beam width is increased. This makes setting the beam parameter much easier. Second, we show how using distance-to-go estimates can allow beam search to find better solutions more quickly in domains with non-uniform costs. Together, these results improve the practical effectiveness of beam search.
Error Analysis and Correction for Weighted A*'s Suboptimality
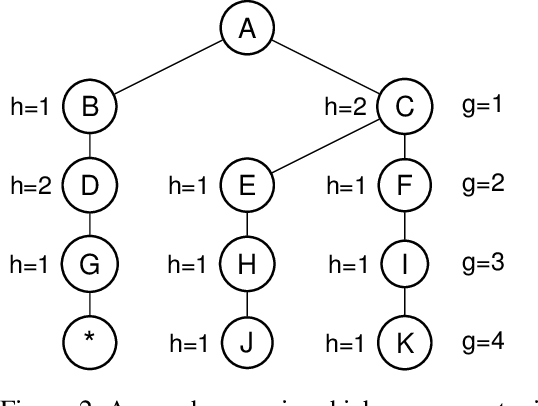
May 27, 2019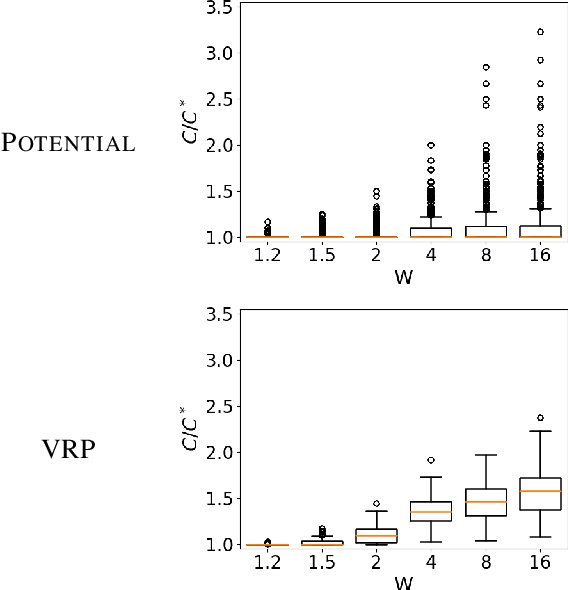
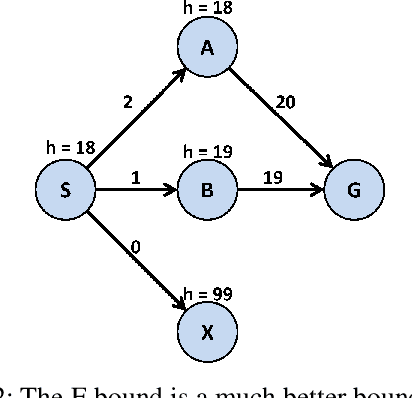
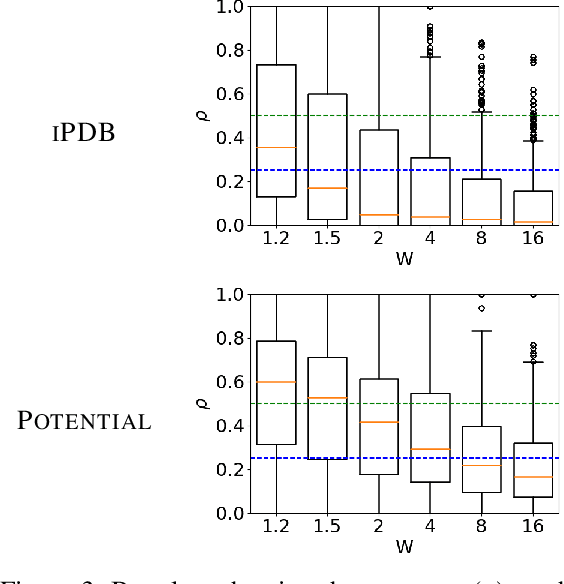
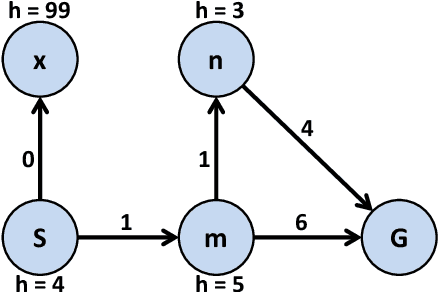
Abstract:Weighted A* (wA*) is a widely used algorithm for rapidly, but suboptimally, solving planning and search problems. The cost of the solution it produces is guaranteed to be at most W times the optimal solution cost, where W is the weight wA* uses in prioritizing open nodes. W is therefore a suboptimality bound for the solution produced by wA*. There is broad consensus that this bound is not very accurate, that the actual suboptimality of wA*'s solution is often much less than W times optimal. However, there is very little published evidence supporting that view, and no existing explanation of why W is a poor bound. This paper fills in these gaps in the literature. We begin with a large-scale experiment demonstrating that, across a wide variety of domains and heuristics for those domains, W is indeed very often far from the true suboptimality of wA*'s solution. We then analytically identify the potential sources of error. Finally, we present a practical method for correcting for two of these sources of error and experimentally show that the correction frequently eliminates much of the error.
An Empirical Study of the Effects of Spurious Transitions on Abstraction-based Heuristics
Nov 14, 2017

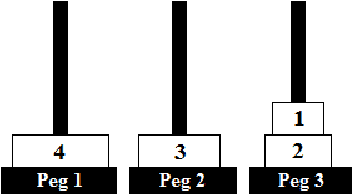

Abstract:The efficient solution of state space search problems is often attempted by guiding search algorithms with heuristics (estimates of the distance from any state to the goal). A popular way for creating heuristic functions is by using an abstract version of the state space. However, the quality of abstraction-based heuristic functions, and thus the speed of search, can suffer from spurious transitions, i.e., state transitions in the abstract state space for which no corresponding transitions in the reachable component of the original state space exist. Our first contribution is a quantitative study demonstrating that the harmful effects of spurious transitions on heuristic functions can be substantial, in terms of both the increase in the number of abstract states and the decrease in the heuristic values, which may slow down search. Our second contribution is an empirical study on the benefits of removing a certain kind of spurious transition, namely those that involve states with a pair of mutually exclusive (mutex) variablevalue assignments. In the context of state space planning, a mutex pair is a pair of variable-value assignments that does not occur in any reachable state. Detecting mutex pairs is a problem that has been addressed frequently in the planning literature. Our study shows that there are cases in which mutex detection helps to eliminate harmful spurious transitions to a large extent and thus to speed up search substantially.
Front-to-End Bidirectional Heuristic Search with Near-Optimal Node Expansions
May 23, 2017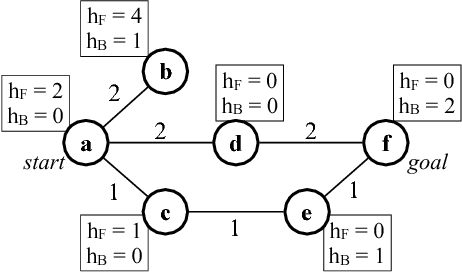
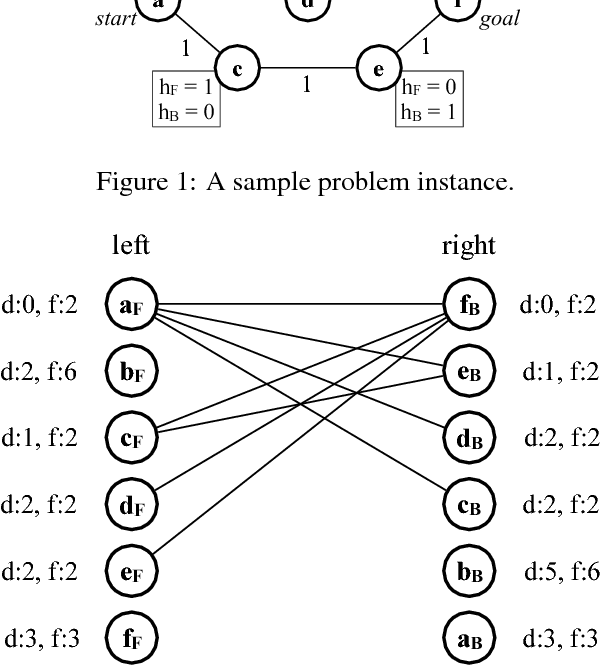
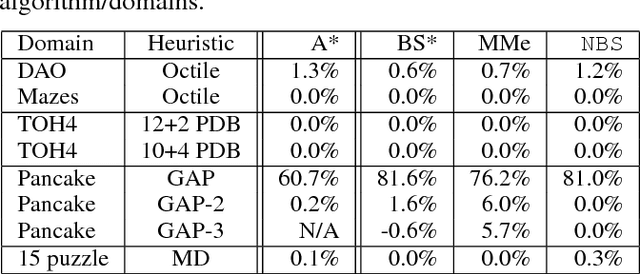
Abstract:It is well-known that any admissible unidirectional heuristic search algorithm must expand all states whose $f$-value is smaller than the optimal solution cost when using a consistent heuristic. Such states are called "surely expanded" (s.e.). A recent study characterized s.e. pairs of states for bidirectional search with consistent heuristics: if a pair of states is s.e. then at least one of the two states must be expanded. This paper derives a lower bound, VC, on the minimum number of expansions required to cover all s.e. pairs, and present a new admissible front-to-end bidirectional heuristic search algorithm, Near-Optimal Bidirectional Search (NBS), that is guaranteed to do no more than 2VC expansions. We further prove that no admissible front-to-end algorithm has a worst case better than 2VC. Experimental results show that NBS competes with or outperforms existing bidirectional search algorithms, and often outperforms A* as well.
Predicting the Performance of IDA* using Conditional Distributions
Jan 15, 2014
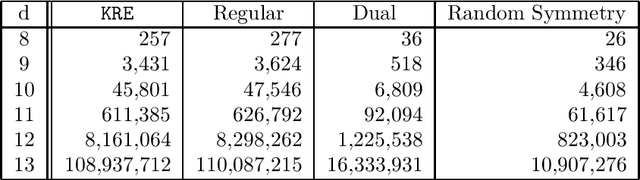
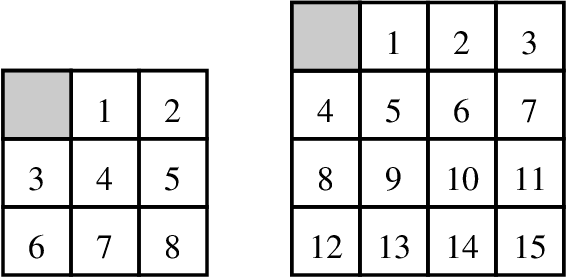
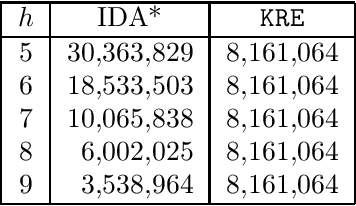
Abstract:Korf, Reid, and Edelkamp introduced a formula to predict the number of nodes IDA* will expand on a single iteration for a given consistent heuristic, and experimentally demonstrated that it could make very accurate predictions. In this paper we show that, in addition to requiring the heuristic to be consistent, their formulas predictions are accurate only at levels of the brute-force search tree where the heuristic values obey the unconditional distribution that they defined and then used in their formula. We then propose a new formula that works well without these requirements, i.e., it can make accurate predictions of IDA*s performance for inconsistent heuristics and if the heuristic values in any level do not obey the unconditional distribution. In order to achieve this we introduce the conditional distribution of heuristic values which is a generalization of their unconditional heuristic distribution. We also provide extensions of our formula that handle individual start states and the augmentation of IDA* with bidirectional pathmax (BPMX), a technique for propagating heuristic values when inconsistent heuristics are used. Experimental results demonstrate the accuracy of our new method and all its variations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge