Evolving A* to Efficiently Solve the k Shortest-Path Problem (Extended Version)

The problem of finding the shortest path in a graph G(V, E) has been widely studied. However, in many applications it is necessary to compute an arbitrary number of them, k. Even though the problem has raised a lot of interest from different research communities and many applications of it are known, it has not been addressed to the same extent as the single shortest path problem. The best algorithm known for efficiently solving this task has a time complexity of O (|E| + |V|log{|V|}+k|V|)$ when computing paths in explicit form, and is based on best-first search. This paper introduces a new search algorithm with the same time complexity, which results from a natural evolution of A* thus, it preserves all its interesting properties, making it widely applicable to many different domains. Experiments in various testbeds show a significant improvement in performance over the state of the art, often by one or two orders of magnitude.

Rectangle Search: An Anytime Beam Search (Extended Version)

Anytime heuristic search algorithms try to find a (potentially suboptimal) solution as quickly as possible and then work to find better and better solutions until an optimal solution is obtained or time is exhausted. The most widely-known anytime search algorithms are based on best-first search. In this paper, we propose a new algorithm, rectangle search, that is instead based on beam search, a variant of breadth-first search. It repeatedly explores alternatives at all depth levels and is thus best-suited to problems featuring deep local minima. Experiments using a variety of popular search benchmarks suggest that rectangle search is competitive with fixed-width beam search and often performs better than the previous best anytime search algorithms.

Beam Search: Faster and Monotonic

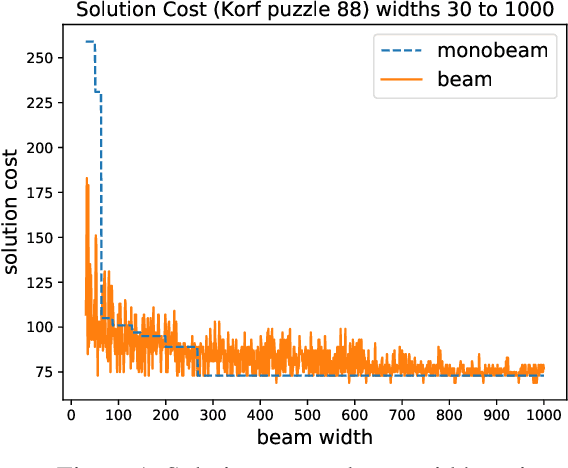
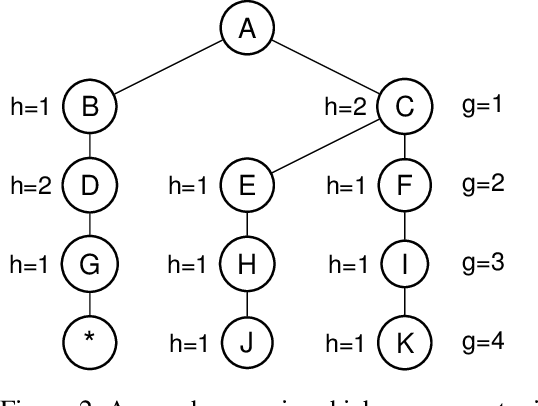
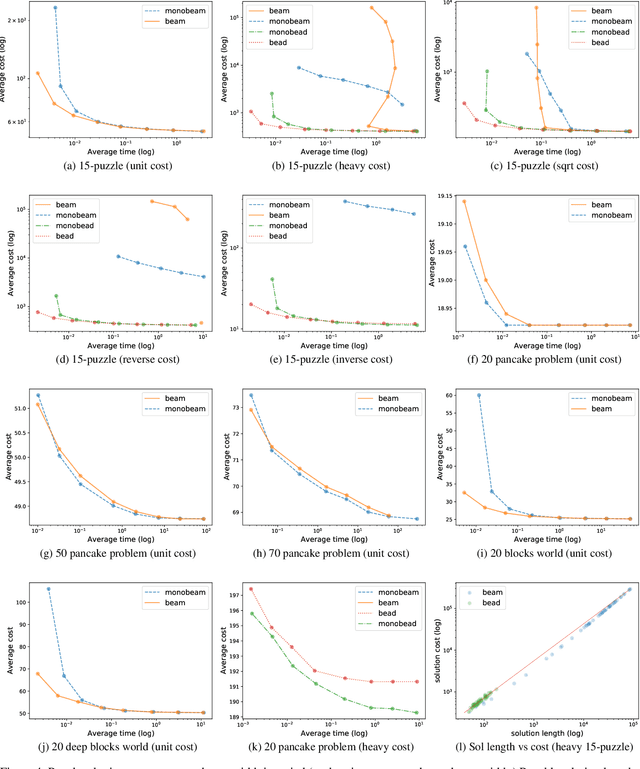
Beam search is a popular satisficing approach to heuristic search problems that allows one to trade increased computation time for lower solution cost by increasing the beam width parameter. We make two contributions to the study of beam search. First, we show how to make beam search monotonic; that is, we provide a new variant that guarantees non-increasing solution cost as the beam width is increased. This makes setting the beam parameter much easier. Second, we show how using distance-to-go estimates can allow beam search to find better solutions more quickly in domains with non-uniform costs. Together, these results improve the practical effectiveness of beam search.