Front-to-End Bidirectional Heuristic Search with Near-Optimal Node Expansions
Paper and Code
May 23, 2017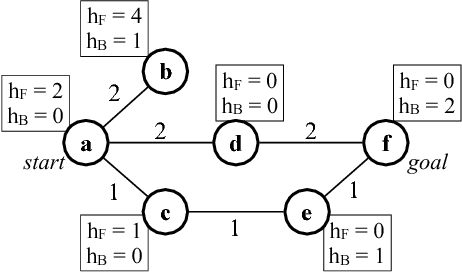
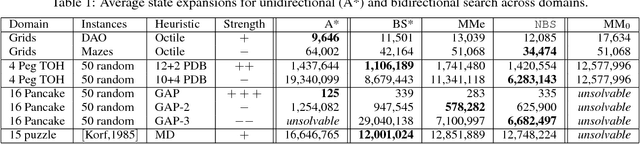
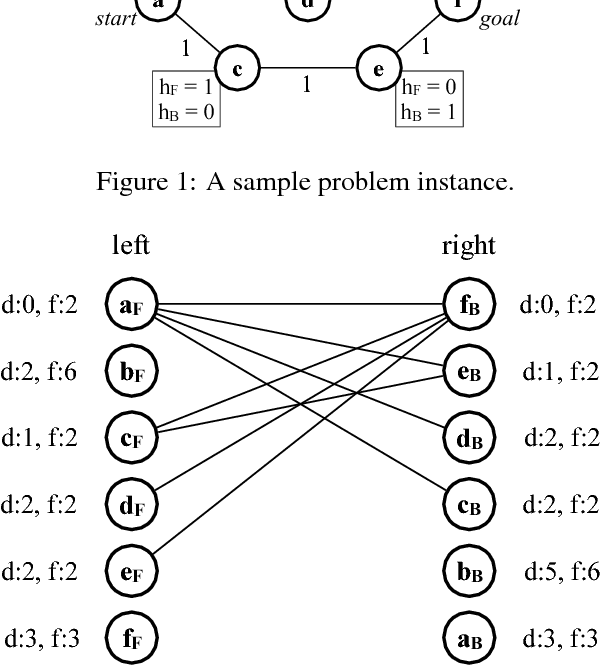
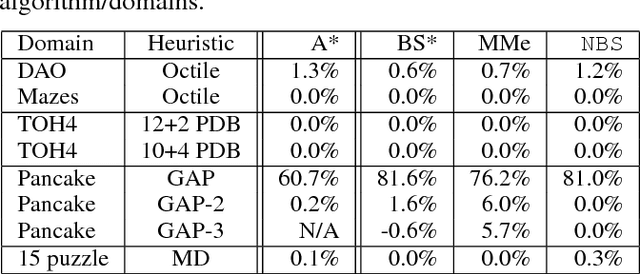
It is well-known that any admissible unidirectional heuristic search algorithm must expand all states whose $f$-value is smaller than the optimal solution cost when using a consistent heuristic. Such states are called "surely expanded" (s.e.). A recent study characterized s.e. pairs of states for bidirectional search with consistent heuristics: if a pair of states is s.e. then at least one of the two states must be expanded. This paper derives a lower bound, VC, on the minimum number of expansions required to cover all s.e. pairs, and present a new admissible front-to-end bidirectional heuristic search algorithm, Near-Optimal Bidirectional Search (NBS), that is guaranteed to do no more than 2VC expansions. We further prove that no admissible front-to-end algorithm has a worst case better than 2VC. Experimental results show that NBS competes with or outperforms existing bidirectional search algorithms, and often outperforms A* as well.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge