Nimrod Segol
Learning Position From Vehicle Vibration Using an Inertial Measurement Unit
Mar 06, 2023Abstract:This paper presents a novel approach to vehicle positioning that operates without reliance on the global navigation satellite system (GNSS). Traditional GNSS approaches are vulnerable to interference in certain environments, rendering them unreliable in situations such as urban canyons, under flyovers, or in low reception areas. This study proposes a vehicle positioning method based on learning the road signature from accelerometer and gyroscope measurements obtained by an inertial measurement unit (IMU) sensor. In our approach, the route is divided into segments, each with a distinct signature that the IMU can detect through the vibrations of a vehicle in response to subtle changes in the road surface. The study presents two different data-driven methods for learning the road segment from IMU measurements. One method is based on convolutional neural networks and the other on ensemble random forest applied to handcrafted features. Additionally, the authors present an algorithm to deduce the position of a vehicle in real-time using the learned road segment. The approach was applied in two positioning tasks: (i) a car along a 6[km] route in a dense urban area; (ii) an e-scooter on a 1[km] route that combined road and pavement surfaces. The mean error between the proposed method's position and the ground truth was approximately 50[m] for the car and 30[m] for the e-scooter. Compared to a solution based on time integration of the IMU measurements, the proposed approach has a mean error of more than 5 times better for e-scooters and 20 times better for cars.
MountNet: Learning an Inertial Sensor Mounting Angle with Deep Neural Networks
Dec 10, 2022



Abstract:Finding the mounting angle of a smartphone inside a car is crucial for navigation, motion detection, activity recognition, and other applications. It is a challenging task in several aspects: (i) the mounting angle at the drive start is unknown and may differ significantly between users; (ii) the user, or bad fixture, may change the mounting angle while driving; (iii) a rapid and computationally efficient real-time solution is required for most applications. To tackle these problems, a data-driven approach using deep neural networks (DNNs) is presented to learn the yaw mounting angle of a smartphone equipped with an inertial measurement unit (IMU) and strapped to a car. The proposed model, MountNet, uses only IMU readings as input and, in contrast to existing solutions, does not require inputs from global navigation satellite systems (GNSS). IMU data is collected for training and validation with the sensor mounted at a known yaw mounting angle and a range of ground truth labels is generated by applying a prescribed rotation to the measurements. Although the training data did not include recordings with real sensor rotations, tests on data with real and synthetic rotations show similar results. An algorithm is formulated for real-time deployment to detect and smooth transitions in device mounting angle estimated by MountNet. MountNet is shown to find the mounting angle rapidly which is critical in real-time applications. Our method converges in less than 30 seconds of driving to a mean error of 4 degrees allowing a fast calibration phase for other algorithms and applications. When the device is rotated in the middle of a drive, large changes converge in 5 seconds and small changes converge in less than 30 seconds.
Improved Convergence Guarantees for Learning Gaussian Mixture Models by EM and Gradient EM
Jan 03, 2021
Abstract:We consider the problem of estimating the parameters a Gaussian Mixture Model with K components of known weights, all with an identity covariance matrix. We make two contributions. First, at the population level, we present a sharper analysis of the local convergence of EM and gradient EM, compared to previous works. Assuming a separation of $\Omega(\sqrt{\log K})$, we prove convergence of both methods to the global optima from an initialization region larger than those of previous works. Specifically, the initial guess of each component can be as far as (almost) half its distance to the nearest Gaussian. This is essentially the largest possible contraction region. Our second contribution are improved sample size requirements for accurate estimation by EM and gradient EM. In previous works, the required number of samples had a quadratic dependence on the maximal separation between the K components, and the resulting error estimate increased linearly with this maximal separation. In this manuscript we show that both quantities depend only logarithmically on the maximal separation.
Set2Graph: Learning Graphs From Sets
Feb 20, 2020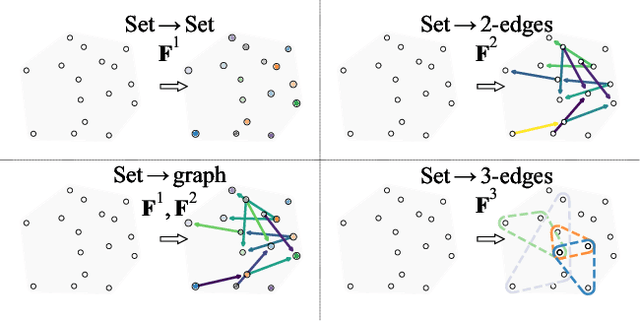
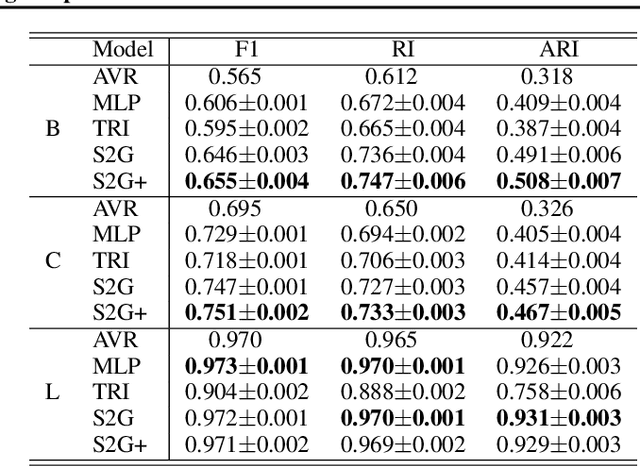
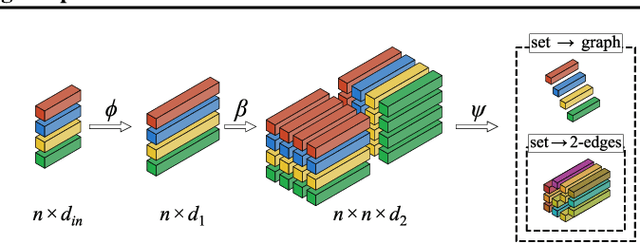
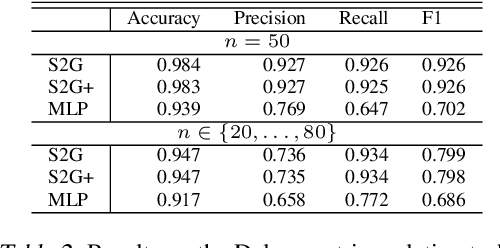
Abstract:Many problems in machine learning (ML) can be cast as learning functions from sets to graphs, or more generally to hypergraphs; in short, Set2Graph functions. Examples include clustering, learning vertex and edge features on graphs, and learning triplet data in a collection. Current neural network models that approximate Set2Graph functions come from two main ML sub-fields: equivariant learning, and similarity learning. Equivariant models would be in general computationally challenging or even infeasible, while similarity learning models can be shown to have limited expressive power. In this paper we suggest a neural network model family for learning Set2Graph functions that is both practical and of maximal expressive power (universal), that is, can approximate arbitrary continuous Set2Graph functions over compact sets. Testing our models on different machine learning tasks, including an application to particle physics, we find them favorable to existing baselines.
On Universal Equivariant Set Networks
Oct 06, 2019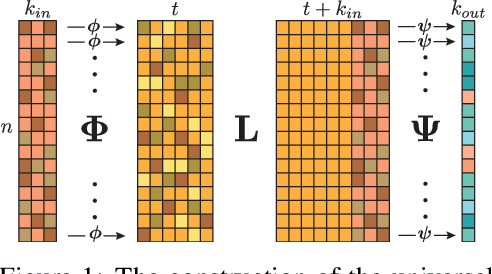
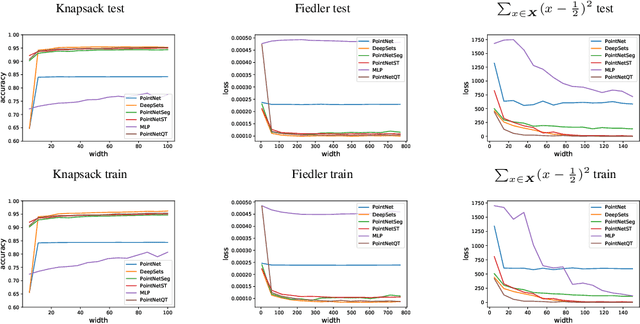
Abstract:Using deep neural networks that are either invariant or equivariant to permutations in order to learn functions on unordered sets has become prevalent. The most popular, basic models are DeepSets [Zaheer et al. 2017] and PointNet [Qi et al. 2017]. While known to be universal for approximating invariant functions, DeepSets and PointNet are not known to be universal when approximating \emph{equivariant} set functions. On the other hand, several recent equivariant set architectures have been proven equivariant universal [Sannai et al. 2019], [Keriven et al. 2019], however these models either use layers that are not permutation equivariant (in the standard sense) and/or use higher order tensor variables which are less practical. There is, therefore, a gap in understanding the universality of popular equivariant set models versus theoretical ones. In this paper we close this gap by proving that: (i) PointNet is not equivariant universal; and (ii) adding a single linear transmission layer makes PointNet universal. We call this architecture PointNetST and argue it is the simplest permutation equivariant universal model known to date. Another consequence is that DeepSets is universal, and also PointNetSeg, a popular point cloud segmentation network (used eg, in [Qi et al. 2017]) is universal. The key theoretical tool used to prove the above results is an explicit characterization of all permutation equivariant polynomial layers. Lastly, we provide numerical experiments validating the theoretical results and comparing different permutation equivariant models.
On the Universality of Invariant Networks
Jan 27, 2019

Abstract:Constraining linear layers in neural networks to respect symmetry transformations from a group $G$ is a common design principle for invariant networks that has found many applications in machine learning. In this paper, we consider a fundamental question that has received little attention to date: Can these networks approximate any (continuous) invariant function? We tackle the rather general case where $G\leq S_n$ (an arbitrary subgroup of the symmetric group) that acts on $\mathbb{R}^n$ by permuting coordinates. This setting includes several recent popular invariant networks. We present two main results: First, $G$-invariant networks are universal if high-order tensors are allowed. Second, there are groups $G$ for which higher-order tensors are unavoidable for obtaining universality. $G$-invariant networks consisting of only first-order tensors are of special interest due to their practical value. We conclude the paper by proving a necessary condition for the universality of $G$-invariant networks that incorporate only first-order tensors. Lastly, we propose a conjecture stating that this condition is also sufficient.
Surface Networks via General Covers
Dec 27, 2018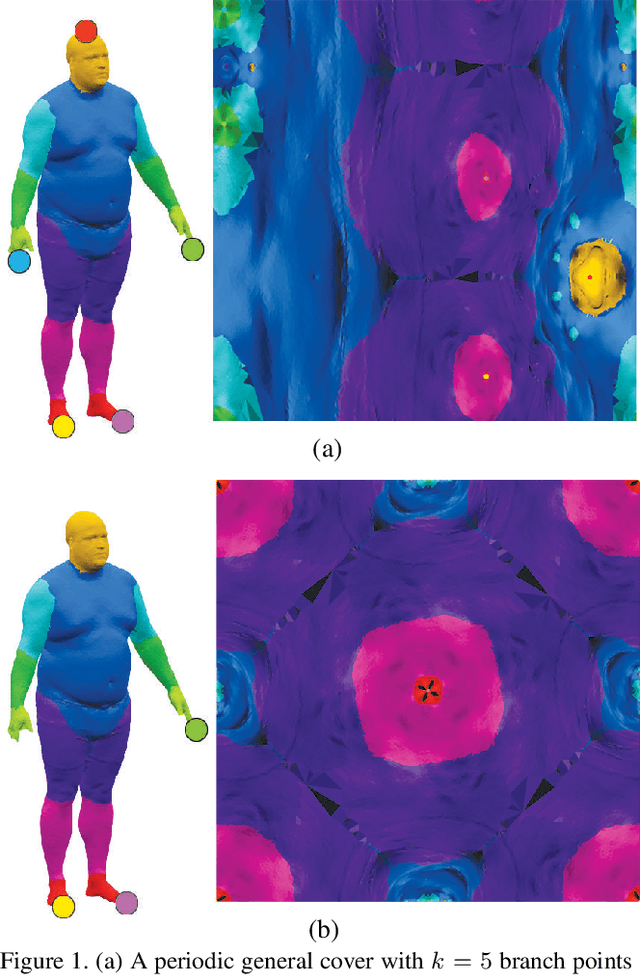
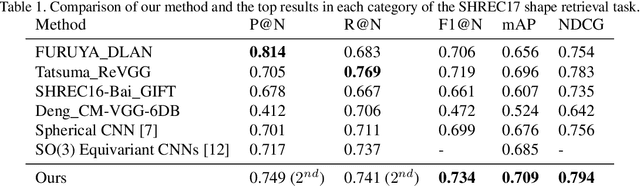
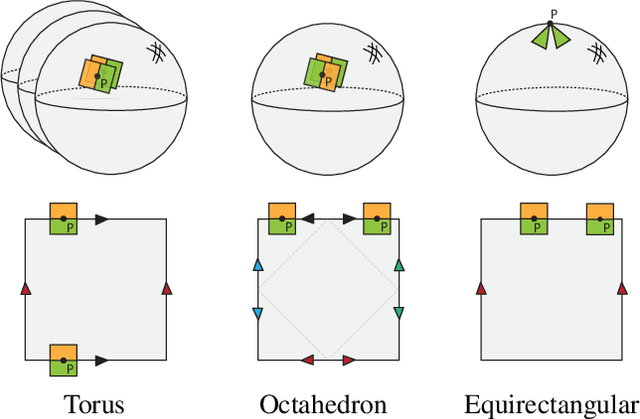
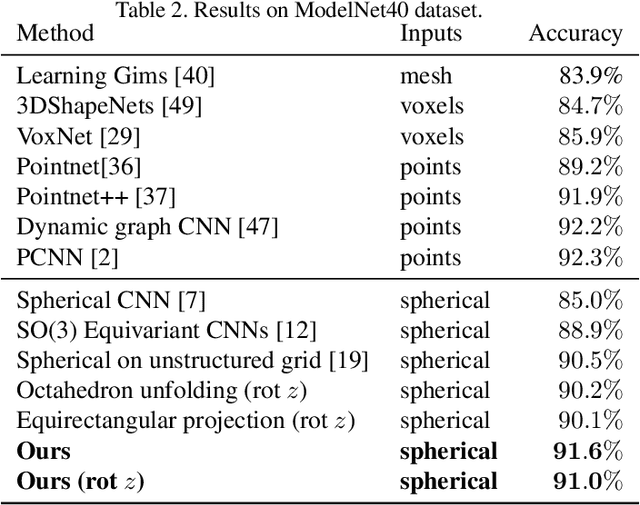
Abstract:Developing deep learning techniques for geometric data is an active and fruitful research area. This paper tackles the problem of sphere-type surface learning by developing a novel surface-to-image representation. Using this representation we are able to quickly adapt successful CNN models to the surface setting. The surface-image representation is based on a covering map from the image domain to the surface. Namely, the map wraps around the surface several times, making sure that every part of the surface is well represented in the image. Differently from previous surface-to-image representations we provide a low distortion coverage of all surface parts in a single image. We have used the surface-to-image representation to apply standard CNN models to the problem of semantic shape segmentation and shape retrieval, achieving state of the art results in both.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge