Hadar Serviansky
Set2Graph: Learning Graphs From Sets
Feb 20, 2020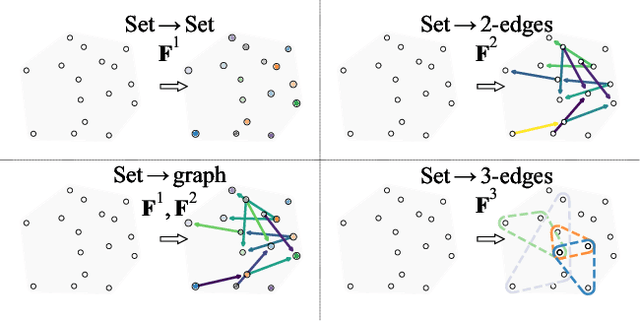
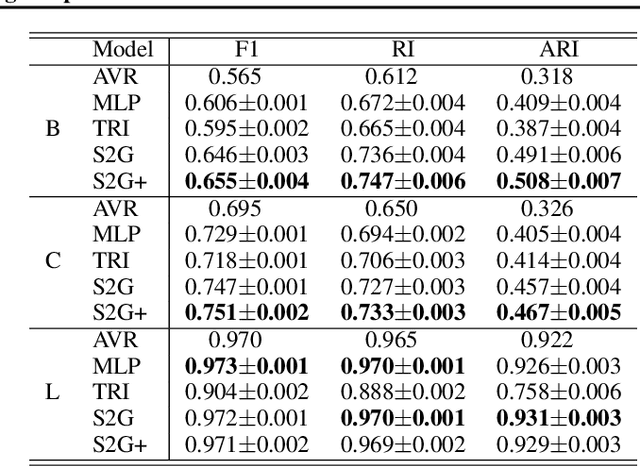
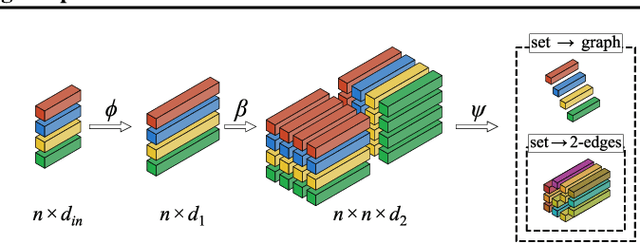
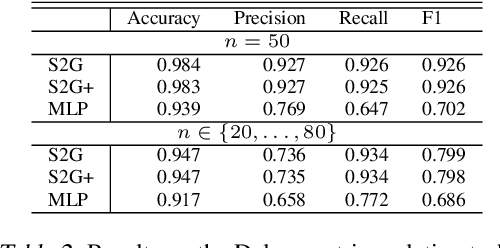
Abstract:Many problems in machine learning (ML) can be cast as learning functions from sets to graphs, or more generally to hypergraphs; in short, Set2Graph functions. Examples include clustering, learning vertex and edge features on graphs, and learning triplet data in a collection. Current neural network models that approximate Set2Graph functions come from two main ML sub-fields: equivariant learning, and similarity learning. Equivariant models would be in general computationally challenging or even infeasible, while similarity learning models can be shown to have limited expressive power. In this paper we suggest a neural network model family for learning Set2Graph functions that is both practical and of maximal expressive power (universal), that is, can approximate arbitrary continuous Set2Graph functions over compact sets. Testing our models on different machine learning tasks, including an application to particle physics, we find them favorable to existing baselines.
Provably Powerful Graph Networks
May 27, 2019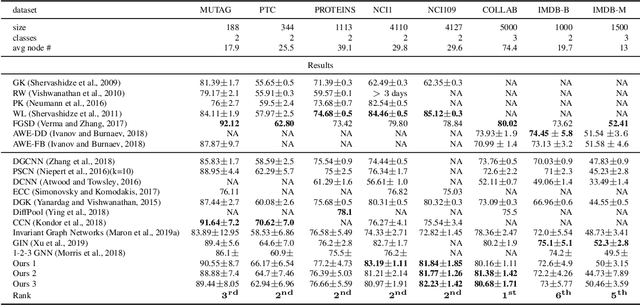
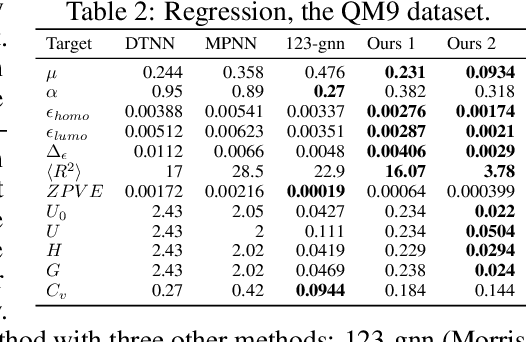
Abstract:Recently, the Weisfeiler-Lehman (WL) graph isomorphism test was used to measure the expressive power of graph neural networks (GNN). It was shown that the popular message passing GNN cannot distinguish between graphs that are indistinguishable by the 1-WL test (Morris et al. 2018; Xu et al. 2019). Unfortunately, many simple instances of graphs are indistinguishable by the 1-WL test. In search for more expressive graph learning models we build upon the recent k-order invariant and equivariant graph neural networks (Maron et al. 2019a,b) and present two results: First, we show that such k-order networks can distinguish between non-isomorphic graphs as good as the k-WL tests, which are provably stronger than the 1-WL test for k>2. This makes these models strictly stronger than message passing models. Unfortunately, the higher expressiveness of these models comes with a computational cost of processing high order tensors. Second, setting our goal at building a provably stronger, simple and scalable model we show that a reduced 2-order network containing just scaled identity operator, augmented with a single quadratic operation (matrix multiplication) has a provable 3-WL expressive power. Differently put, we suggest a simple model that interleaves applications of standard Multilayer-Perceptron (MLP) applied to the feature dimension and matrix multiplication. We validate this model by presenting state of the art results on popular graph classification and regression tasks. To the best of our knowledge, this is the first practical invariant/equivariant model with guaranteed 3-WL expressiveness, strictly stronger than message passing models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge