Injective Sliced-Wasserstein embedding for weighted sets and point clouds
Paper and Code
May 26, 2024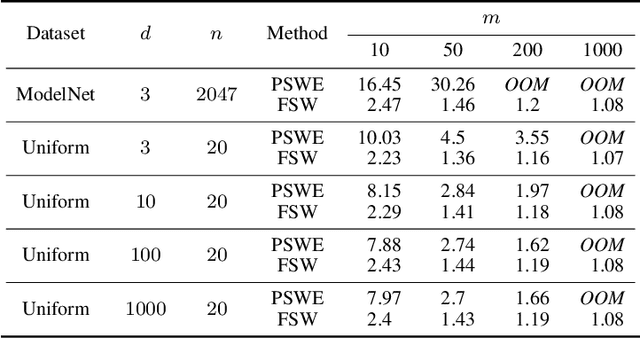
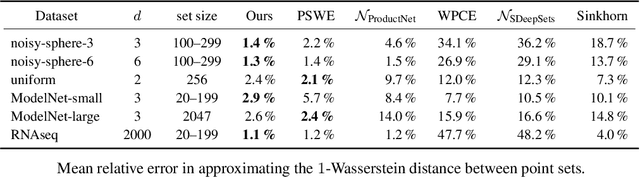
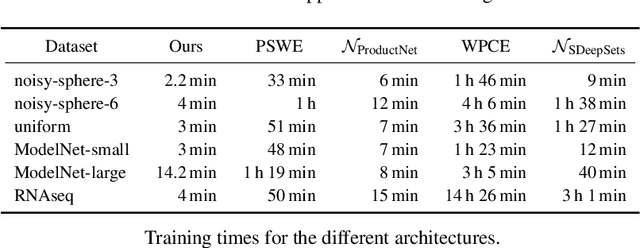
We present the $\textit{Sliced Wasserstein Embedding}$ $\unicode{x2014}$ a novel method to embed multisets and distributions over $\mathbb{R}^d$ into Euclidean space. Our embedding is injective and approximately preserves the Sliced Wasserstein distance. Moreover, when restricted to multisets, it is bi-Lipschitz. We also prove that it is $\textit{impossible}$ to embed distributions over $\mathbb{R}^d$ into a Euclidean space in a bi-Lipschitz manner, even under the assumption that their support is bounded and finite. We demonstrate empirically that our embedding offers practical advantage in learning tasks over existing methods for handling multisets.
* 28 pages
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge