FSW-GNN: A Bi-Lipschitz WL-Equivalent Graph Neural Network

Many of the most popular graph neural networks fall into the category of message-passing neural networks (MPNNs). Famously, MPNNs' ability to distinguish between graphs is limited to graphs separable by the Weisfeiler-Lemann (WL) graph isomorphism test, and the strongest MPNNs, in terms of separation power, are WL-equivalent. Recently, it was shown that the quality of separation provided by standard WL-equivalent MPNN can be very low, resulting in WL-separable graphs being mapped to very similar, hardly distinguishable features. This paper addresses this issue by seeking bi-Lipschitz continuity guarantees for MPNNs. We demonstrate that, in contrast with standard summation-based MPNNs, which lack bi-Lipschitz properties, our proposed model provides a bi-Lipschitz graph embedding with respect to two standard graph metrics. Empirically, we show that our MPNN is competitive with standard MPNNs for several graph learning tasks and is far more accurate in over-squashing long-range tasks.

Revisiting Multi-Permutation Equivariance through the Lens of Irreducible Representations

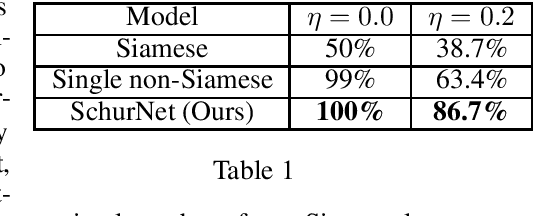
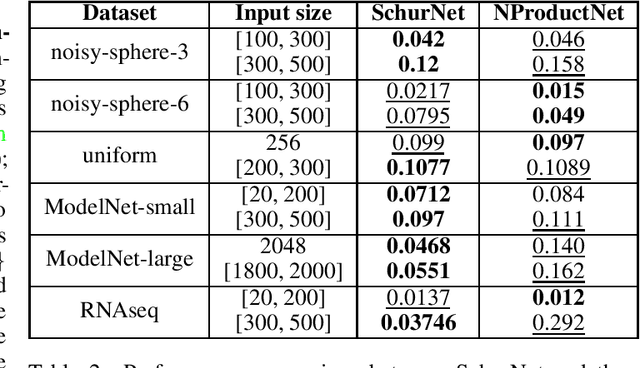
This paper explores the characterization of equivariant linear layers for representations of permutations and related groups. Unlike traditional approaches, which address these problems using parameter-sharing, we consider an alternative methodology based on irreducible representations and Schur's lemma. Using this methodology, we obtain an alternative derivation for existing models like DeepSets, 2-IGN graph equivariant networks, and Deep Weight Space (DWS) networks. The derivation for DWS networks is significantly simpler than that of previous results. Next, we extend our approach to unaligned symmetric sets, where equivariance to the wreath product of groups is required. Previous works have addressed this problem in a rather restrictive setting, in which almost all wreath equivariant layers are Siamese. In contrast, we give a full characterization of layers in this case and show that there is a vast number of additional non-Siamese layers in some settings. We also show empirically that these additional non-Siamese layers can improve performance in tasks like graph anomaly detection, weight space alignment, and learning Wasserstein distances. Our code is available at \href{https://github.com/yonatansverdlov/Irreducible-Representations-of-Deep-Weight-Spaces}{GitHub}.

On the Expressive Power of Sparse Geometric MPNNs

Motivated by applications in chemistry and other sciences, we study the expressive power of message-passing neural networks for geometric graphs, whose node features correspond to 3-dimensional positions. Recent work has shown that such models can separate generic pairs of non-equivalent geometric graphs, though they may fail to separate some rare and complicated instances. However, these results assume a fully connected graph, where each node possesses complete knowledge of all other nodes. In contrast, often, in application, every node only possesses knowledge of a small number of nearest neighbors. This paper shows that generic pairs of non-equivalent geometric graphs can be separated by message-passing networks with rotation equivariant features as long as the underlying graph is connected. When only invariant intermediate features are allowed, generic separation is guaranteed for generically globally rigid graphs. We introduce a simple architecture, EGENNET, which achieves our theoretical guarantees and compares favorably with alternative architecture on synthetic and chemical benchmarks.

Efficient Rehearsal Free Zero Forgetting Continual Learning using Adaptive Weight Modulation

Artificial neural networks encounter a notable challenge known as continual learning, which involves acquiring knowledge of multiple tasks over an extended period. This challenge arises due to the tendency of previously learned weights to be adjusted to suit the objectives of new tasks, resulting in a phenomenon called catastrophic forgetting. Most approaches to this problem seek a balance between maximizing performance on the new tasks and minimizing the forgetting of previous tasks. In contrast, our approach attempts to maximize the performance of the new task, while ensuring zero forgetting. This is accomplished by creating a task-specific modulation parameters for each task. Only these would be learnable parameters during learning of consecutive tasks. Through comprehensive experimental evaluations, our model demonstrates superior performance in acquiring and retaining novel tasks that pose difficulties for other multi-task models. This emphasizes the efficacy of our approach in preventing catastrophic forgetting while accommodating the acquisition of new tasks