Neural Injective Functions for Multisets, Measures and Graphs via a Finite Witness Theorem

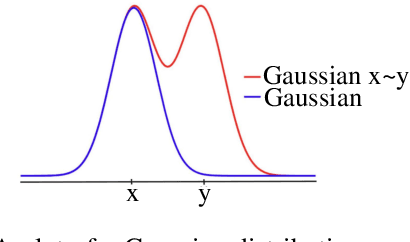
Injective multiset functions have a key role in the theoretical study of machine learning on multisets and graphs. Yet, there remains a gap between the provably injective multiset functions considered in theory, which typically rely on polynomial moments, and the multiset functions used in practice which typically rely on $\textit{neural moments}$, whose injectivity on multisets has not been studied to date. In this paper we bridge this gap by showing that moments of neural network do define an injective multiset function, provided that an analytic non-polynomial activation is used. The number of moments required by our theory is optimal up to a multiplicative factor of two. To prove this result, we state and prove a $\textit{finite witness theorem}$, which is of independent interest. As a corollary to our main theorem, we derive new approximation results for functions on multisets and measures, and new separation results for graph neural networks. We also provide two negative results: We show that (1) moments of piecewise-linear neural networks do not lead to injective multiset functions, and (2) even when moment-based multiset functions are injective, they will never be bi-Lipschitz.

Complete Neural Networks for Euclidean Graphs

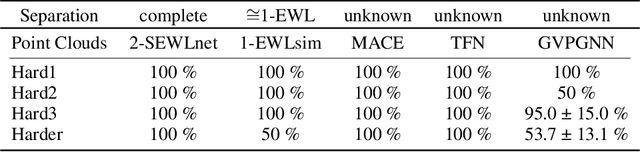
We propose a 2-WL-like geometric graph isomorphism test and prove it is complete when applied to Euclidean Graphs in $\mathbb{R}^3$. We then use recent results on multiset embeddings to devise an efficient geometric GNN model with equivalent separation power. We verify empirically that our GNN model is able to separate particularly challenging synthetic examples, and demonstrate its usefulness for a chemical property prediction problem.

Low Dimensional Invariant Embeddings for Universal Geometric Learning

This paper studies separating invariants: mappings on $d$-dimensional semi-algebraic subsets of $D$ dimensional Euclidean domains which are invariant to semi-algebraic group actions and separate orbits. The motivation for this study comes from the usefulness of separating invariants in proving universality of equivariant neural network architectures. We observe that in several cases the cardinality of separating invariants proposed in the machine learning literature is much larger than the ambient dimension $D$. As a result, the theoretical universal constructions based on these separating invariants is unrealistically large. Our goal in this paper is to resolve this issue. We show that when a continuous family of semi-algebraic separating invariants is available, separation can be obtained by randomly selecting $2d+1 $ of these invariants. We apply this methodology to obtain an efficient scheme for computing separating invariants for several classical group actions which have been studied in the invariant learning literature. Examples include matrix multiplication actions on point clouds by permutations, rotations, and various other linear groups.

Unique Geometry and Texture from Corresponding Image Patches

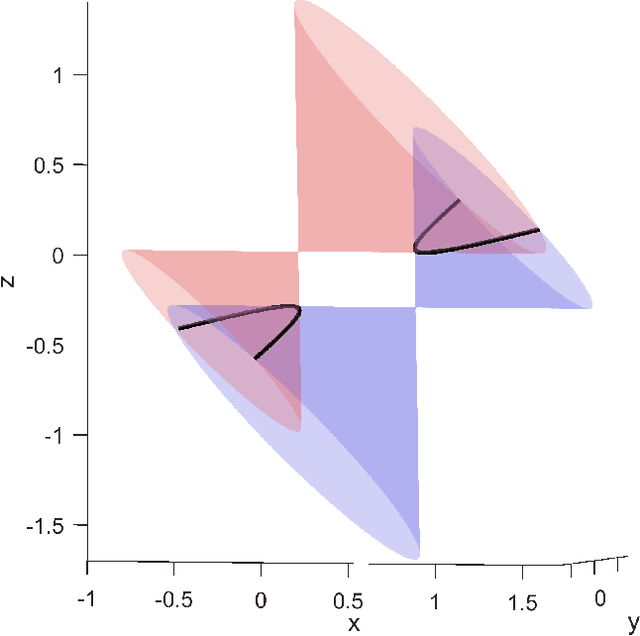
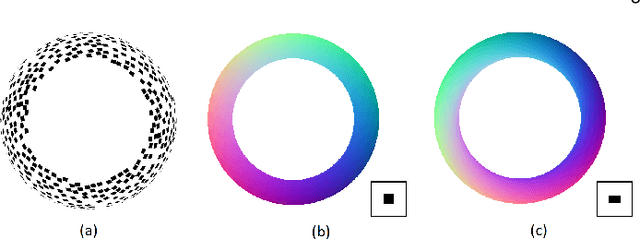
We present a sufficient condition for the recovery of a unique texture process and a unique set of viewpoints from a set of image patches that are generated by observing a flat texture process from unknown directions and orientations. We show that four image patches are sufficient in general, and we characterize the ambiguities that arise when this condition is not satisfied. The results are applicable to the perception of shape from texture and to texture-based structure from motion.

Low-level Vision by Consensus in a Spatial Hierarchy of Regions

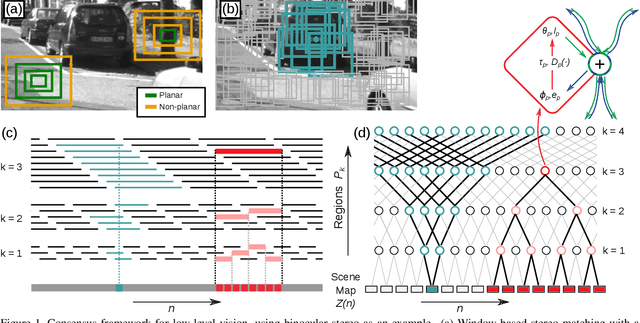
We introduce a multi-scale framework for low-level vision, where the goal is estimating physical scene values from image data---such as depth from stereo image pairs. The framework uses a dense, overlapping set of image regions at multiple scales and a "local model," such as a slanted-plane model for stereo disparity, that is expected to be valid piecewise across the visual field. Estimation is cast as optimization over a dichotomous mixture of variables, simultaneously determining which regions are inliers with respect to the local model (binary variables) and the correct co-ordinates in the local model space for each inlying region (continuous variables). When the regions are organized into a multi-scale hierarchy, optimization can occur in an efficient and parallel architecture, where distributed computational units iteratively perform calculations and share information through sparse connections between parents and children. The framework performs well on a standard benchmark for binocular stereo, and it produces a distributional scene representation that is appropriate for combining with higher-level reasoning and other low-level cues.

From Shading to Local Shape

We develop a framework for extracting a concise representation of the shape information available from diffuse shading in a small image patch. This produces a mid-level scene descriptor, comprised of local shape distributions that are inferred separately at every image patch across multiple scales. The framework is based on a quadratic representation of local shape that, in the absence of noise, has guarantees on recovering accurate local shape and lighting. And when noise is present, the inferred local shape distributions provide useful shape information without over-committing to any particular image explanation. These local shape distributions naturally encode the fact that some smooth diffuse regions are more informative than others, and they enable efficient and robust reconstruction of object-scale shape. Experimental results show that this approach to surface reconstruction compares well against the state-of-art on both synthetic images and captured photographs.