Detecting Arbitrary Planted Subgraphs in Random Graphs

The problems of detecting and recovering planted structures/subgraphs in Erd\H{o}s-R\'{e}nyi random graphs, have received significant attention over the past three decades, leading to many exciting results and mathematical techniques. However, prior work has largely focused on specific ad hoc planted structures and inferential settings, while a general theory has remained elusive. In this paper, we bridge this gap by investigating the detection of an \emph{arbitrary} planted subgraph $\Gamma = \Gamma_n$ in an Erd\H{o}s-R\'{e}nyi random graph $\mathcal{G}(n, q_n)$, where the edge probability within $\Gamma$ is $p_n$. We examine both the statistical and computational aspects of this problem and establish the following results. In the dense regime, where the edge probabilities $p_n$ and $q_n$ are fixed, we tightly characterize the information-theoretic and computational thresholds for detecting $\Gamma$, and provide conditions under which a computational-statistical gap arises. Most notably, these thresholds depend on $\Gamma$ only through its number of edges, maximum degree, and maximum subgraph density. Our lower and upper bounds are general and apply to any value of $p_n$ and $q_n$ as functions of $n$. Accordingly, we also analyze the sparse regime where $q_n = \Theta(n^{-\alpha})$ and $p_n-q_n =\Theta(q_n)$, with $\alpha\in[0,2]$, as well as the critical regime where $p_n=1-o(1)$ and $q_n = \Theta(n^{-\alpha})$, both of which have been widely studied, for specific choices of $\Gamma$. For these regimes, we show that our bounds are tight for all planted subgraphs investigated in the literature thus far\textemdash{}and many more. Finally, we identify conditions under which detection undergoes sharp phase transition, where the boundaries at which algorithms succeed or fail shift abruptly as a function of $q_n$.

Detection of Correlated Random Vectors

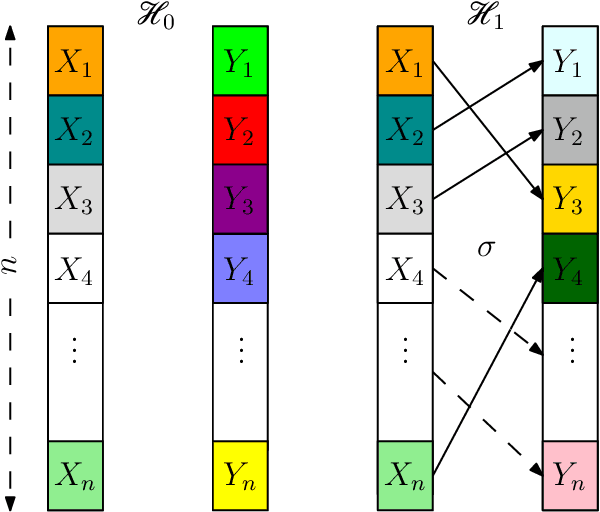
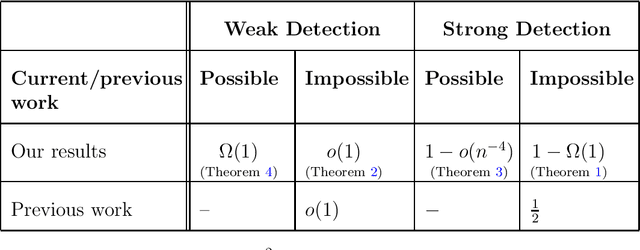
In this paper, we investigate the problem of deciding whether two standard normal random vectors $\mathsf{X}\in\mathbb{R}^{n}$ and $\mathsf{Y}\in\mathbb{R}^{n}$ are correlated or not. This is formulated as a hypothesis testing problem, where under the null hypothesis, these vectors are statistically independent, while under the alternative, $\mathsf{X}$ and a randomly and uniformly permuted version of $\mathsf{Y}$, are correlated with correlation $\rho$. We analyze the thresholds at which optimal testing is information-theoretically impossible and possible, as a function of $n$ and $\rho$. To derive our information-theoretic lower bounds, we develop a novel technique for evaluating the second moment of the likelihood ratio using an orthogonal polynomials expansion, which among other things, reveals a surprising connection to integer partition functions. We also study a multi-dimensional generalization of the above setting, where rather than two vectors we observe two databases/matrices, and furthermore allow for partial correlations between these two.

Phase Transitions in the Detection of Correlated Databases

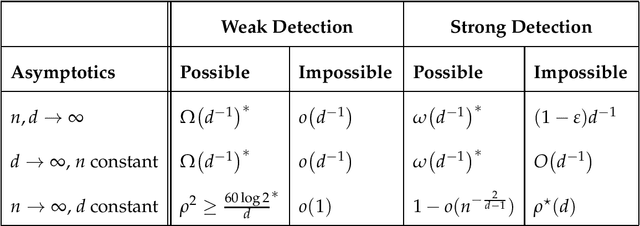
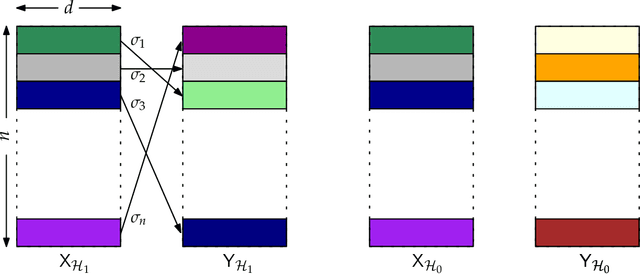
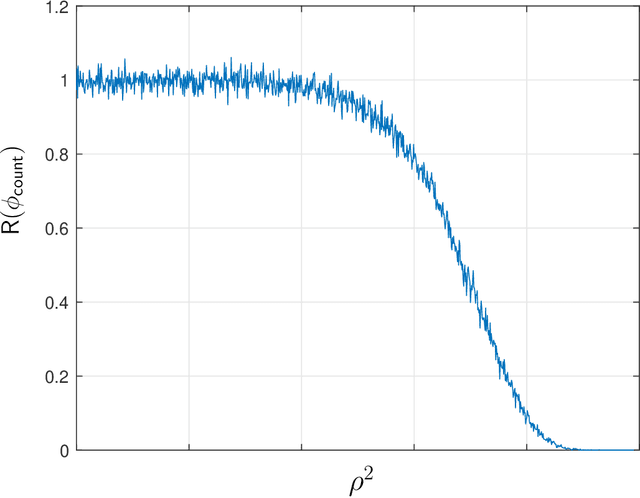
We study the problem of detecting the correlation between two Gaussian databases $\mathsf{X}\in\mathbb{R}^{n\times d}$ and $\mathsf{Y}^{n\times d}$, each composed of $n$ users with $d$ features. This problem is relevant in the analysis of social media, computational biology, etc. We formulate this as a hypothesis testing problem: under the null hypothesis, these two databases are statistically independent. Under the alternative, however, there exists an unknown permutation $\sigma$ over the set of $n$ users (or, row permutation), such that $\mathsf{X}$ is $\rho$-correlated with $\mathsf{Y}^\sigma$, a permuted version of $\mathsf{Y}$. We determine sharp thresholds at which optimal testing exhibits a phase transition, depending on the asymptotic regime of $n$ and $d$. Specifically, we prove that if $\rho^2d\to0$, as $d\to\infty$, then weak detection (performing slightly better than random guessing) is statistically impossible, irrespectively of the value of $n$. This compliments the performance of a simple test that thresholds the sum all entries of $\mathsf{X}^T\mathsf{Y}$. Furthermore, when $d$ is fixed, we prove that strong detection (vanishing error probability) is impossible for any $\rho<\rho^\star$, where $\rho^\star$ is an explicit function of $d$, while weak detection is again impossible as long as $\rho^2d\to0$. These results close significant gaps in current recent related studies.