From Features to Transformers: Redefining Ranking for Scalable Impact

We present LiGR, a large-scale ranking framework developed at LinkedIn that brings state-of-the-art transformer-based modeling architectures into production. We introduce a modified transformer architecture that incorporates learned normalization and simultaneous set-wise attention to user history and ranked items. This architecture enables several breakthrough achievements, including: (1) the deprecation of most manually designed feature engineering, outperforming the prior state-of-the-art system using only few features (compared to hundreds in the baseline), (2) validation of the scaling law for ranking systems, showing improved performance with larger models, more training data, and longer context sequences, and (3) simultaneous joint scoring of items in a set-wise manner, leading to automated improvements in diversity. To enable efficient serving of large ranking models, we describe techniques to scale inference effectively using single-pass processing of user history and set-wise attention. We also summarize key insights from various ablation studies and A/B tests, highlighting the most impactful technical approaches.

A Precise Characterization of SGD Stability Using Loss Surface Geometry

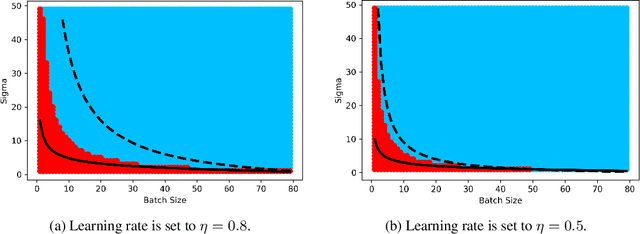
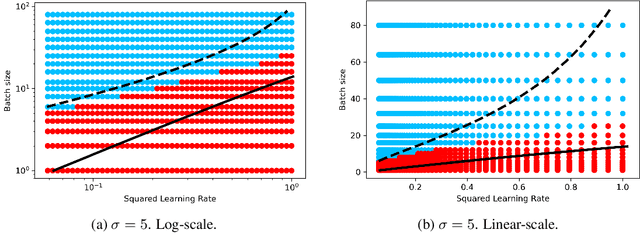
Stochastic Gradient Descent (SGD) stands as a cornerstone optimization algorithm with proven real-world empirical successes but relatively limited theoretical understanding. Recent research has illuminated a key factor contributing to its practical efficacy: the implicit regularization it instigates. Several studies have investigated the linear stability property of SGD in the vicinity of a stationary point as a predictive proxy for sharpness and generalization error in overparameterized neural networks (Wu et al., 2022; Jastrzebski et al., 2019; Cohen et al., 2021). In this paper, we delve deeper into the relationship between linear stability and sharpness. More specifically, we meticulously delineate the necessary and sufficient conditions for linear stability, contingent on hyperparameters of SGD and the sharpness at the optimum. Towards this end, we introduce a novel coherence measure of the loss Hessian that encapsulates pertinent geometric properties of the loss function that are relevant to the linear stability of SGD. It enables us to provide a simplified sufficient condition for identifying linear instability at an optimum. Notably, compared to previous works, our analysis relies on significantly milder assumptions and is applicable for a broader class of loss functions than known before, encompassing not only mean-squared error but also cross-entropy loss.

mSAM: Micro-Batch-Averaged Sharpness-Aware Minimization

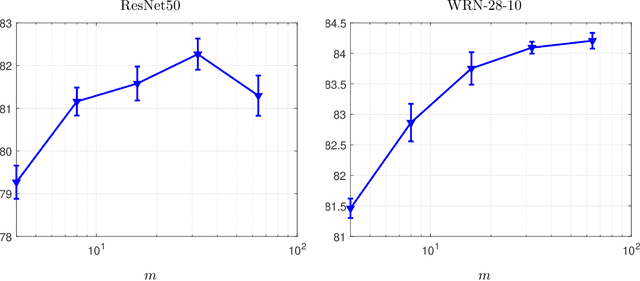
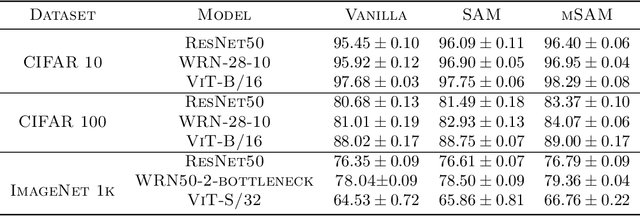
Modern deep learning models are over-parameterized, where different optima can result in widely varying generalization performance. To account for this, Sharpness-Aware Minimization (SAM) modifies the underlying loss function to guide descent methods towards flatter minima, which arguably have better generalization abilities. In this paper, we focus on a variant of SAM known as micro-batch SAM (mSAM), which, during training, averages the updates generated by adversarial perturbations across several disjoint shards (micro batches) of a mini-batch. We extend a recently developed and well-studied general framework for flatness analysis to show that distributed gradient computation for sharpness-aware minimization theoretically achieves even flatter minima. In order to support this theoretical superiority, we provide a thorough empirical evaluation on a variety of image classification and natural language processing tasks. We also show that contrary to previous work, mSAM can be implemented in a flexible and parallelizable manner without significantly increasing computational costs. Our practical implementation of mSAM yields superior generalization performance across a wide range of tasks compared to SAM, further supporting our theoretical framework.