Isometric Graph Neural Networks
Paper and Code
Jun 16, 2020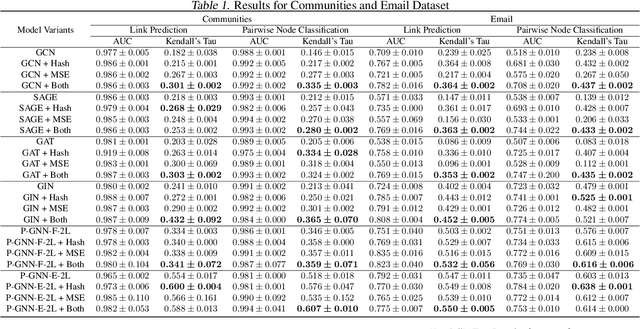
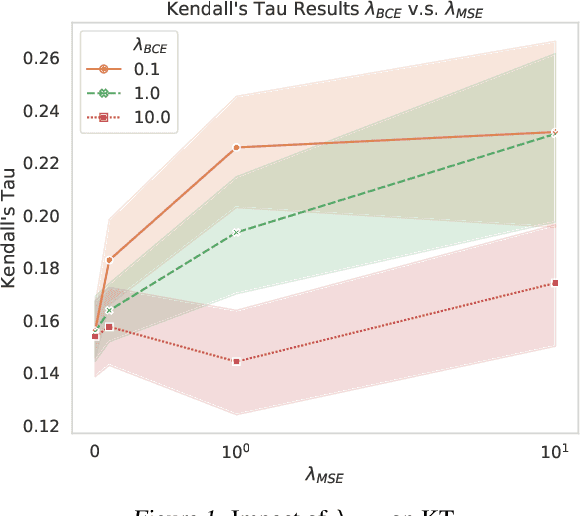
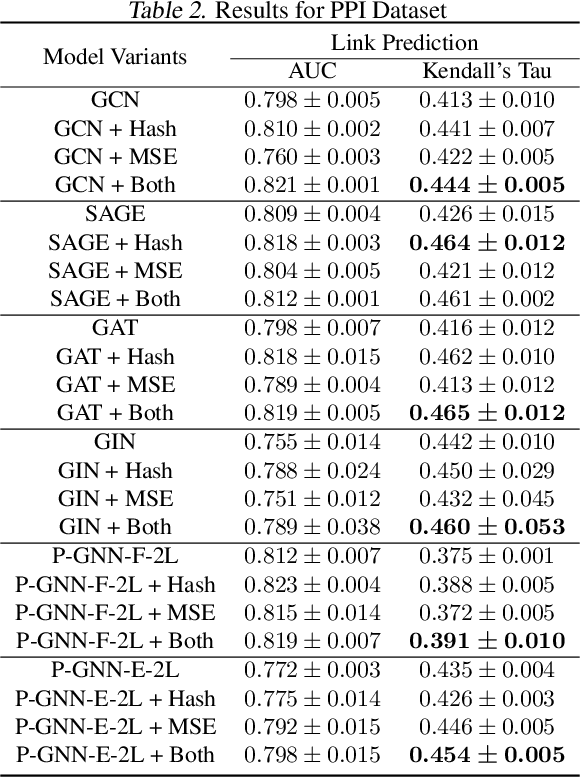
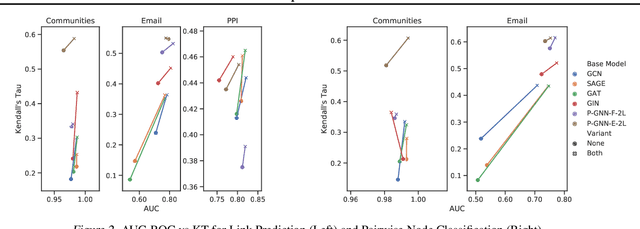
Many tasks that rely on representations of nodes in graphs would benefit if those representations were faithful to distances between nodes in the graph. Geometric techniques to extract such representations have poor scaling over large graph size, and recent advances in Graph Neural Network (GNN) algorithms have limited ability to reflect graph distance information beyond the first degree neighborhood. To enable this highly desired capability, we propose a technique to learn Isometric Graph Neural Networks (IGNN), which requires changing the input representation space and loss function to enable any GNN algorithm to generate representations that reflect distances between nodes. We experiment with the isometric technique on several GNN architectures for modeling multiple prediction tasks on multiple datasets. In addition to an improvement in AUC-ROC as high as $43\%$ in these experiments, we observe a consistent and substantial improvement as high as 400% in Kendall's Tau (KT), a measure that directly reflects distance information, demonstrating that the learned embeddings do account for graph distances.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge