Yiou Xiao
AdaGNN: A multi-modal latent representation meta-learner for GNNs based on AdaBoosting
Aug 14, 2021



Abstract:As a special field in deep learning, Graph Neural Networks (GNNs) focus on extracting intrinsic network features and have drawn unprecedented popularity in both academia and industry. Most of the state-of-the-art GNN models offer expressive, robust, scalable and inductive solutions empowering social network recommender systems with rich network features that are computationally difficult to leverage with graph traversal based methods. Most recent GNNs follow an encoder-decoder paradigm to encode high dimensional heterogeneous information from a subgraph onto one low dimensional embedding space. However, one single embedding space usually fails to capture all aspects of graph signals. In this work, we propose boosting-based meta learner for GNNs, which automatically learns multiple projections and the corresponding embedding spaces that captures different aspects of the graph signals. As a result, similarities between sub-graphs are quantified by embedding proximity on multiple embedding spaces. AdaGNN performs exceptionally well for applications with rich and diverse node neighborhood information. Moreover, AdaGNN is compatible with any inductive GNNs for both node-level and edge-level tasks.
Isometric Graph Neural Networks
Jun 16, 2020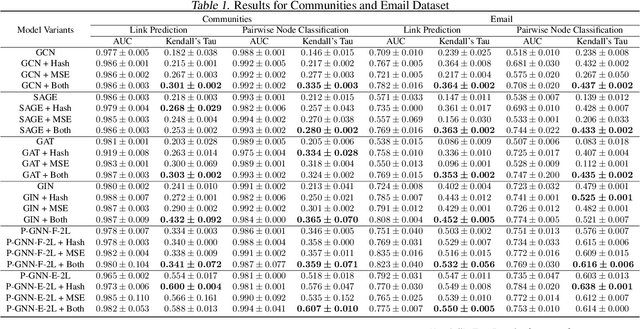
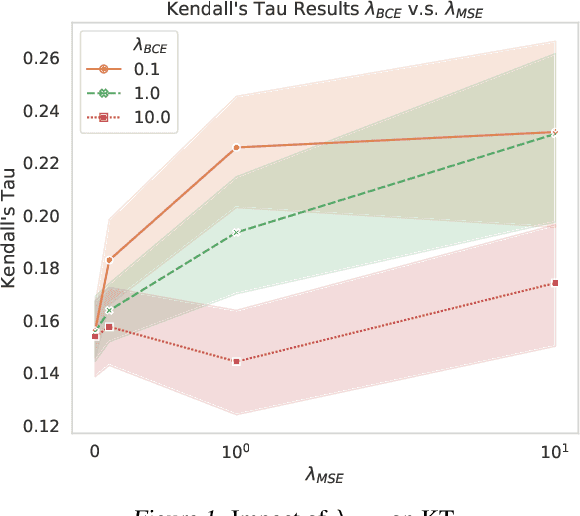
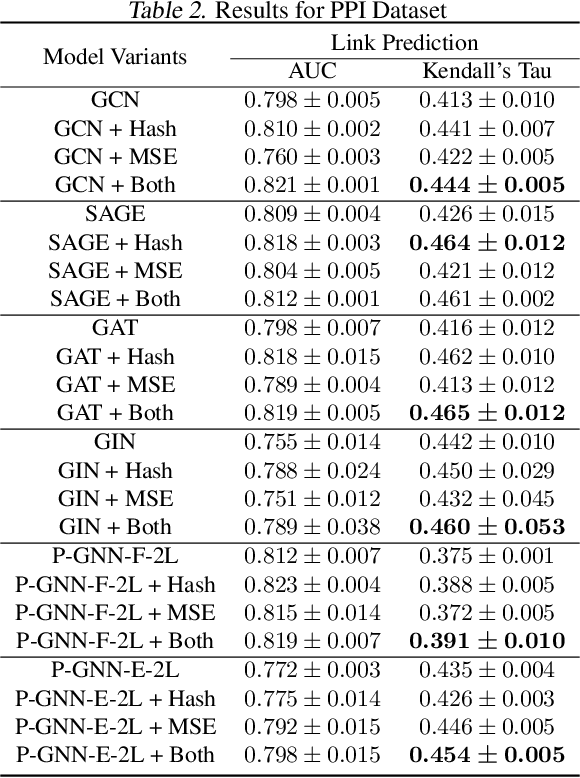
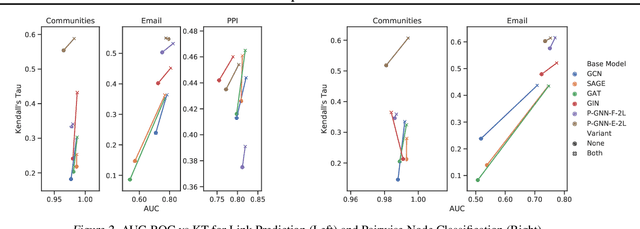
Abstract:Many tasks that rely on representations of nodes in graphs would benefit if those representations were faithful to distances between nodes in the graph. Geometric techniques to extract such representations have poor scaling over large graph size, and recent advances in Graph Neural Network (GNN) algorithms have limited ability to reflect graph distance information beyond the first degree neighborhood. To enable this highly desired capability, we propose a technique to learn Isometric Graph Neural Networks (IGNN), which requires changing the input representation space and loss function to enable any GNN algorithm to generate representations that reflect distances between nodes. We experiment with the isometric technique on several GNN architectures for modeling multiple prediction tasks on multiple datasets. In addition to an improvement in AUC-ROC as high as $43\%$ in these experiments, we observe a consistent and substantial improvement as high as 400% in Kendall's Tau (KT), a measure that directly reflects distance information, demonstrating that the learned embeddings do account for graph distances.
Relation Learning on Social Networks with Multi-Modal Graph Edge Variational Autoencoders
Nov 04, 2019



Abstract:While node semantics have been extensively explored in social networks, little research attention has been paid to profile edge semantics, i.e., social relations. Ideal edge semantics should not only show that two users are connected, but also why they know each other and what they share in common. However, relations in social networks are often hard to profile, due to noisy multi-modal signals and limited user-generated ground-truth labels. In this work, we aim to develop a unified and principled framework that can profile user relations as edge semantics in social networks by integrating multi-modal signals in the presence of noisy and incomplete data. Our framework is also flexible towards limited or missing supervision. Specifically, we assume a latent distribution of multiple relations underlying each user link, and learn them with multi-modal graph edge variational autoencoders. We encode the network data with a graph convolutional network, and decode arbitrary signals with multiple reconstruction networks. Extensive experiments and case studies on two public DBLP author networks and two internal LinkedIn member networks demonstrate the superior effectiveness and efficiency of our proposed model.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge