Nonparametric Bayesian Factor Analysis for Dynamic Count Matrices
Paper and Code
Dec 30, 2015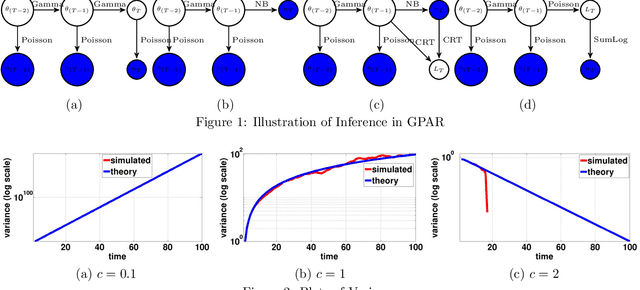
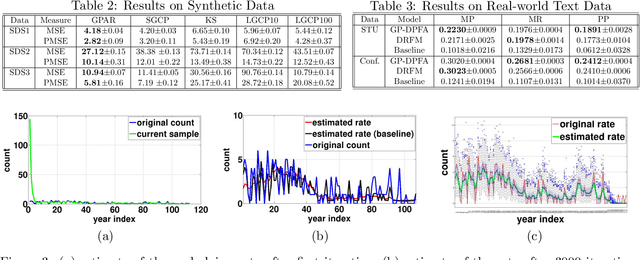
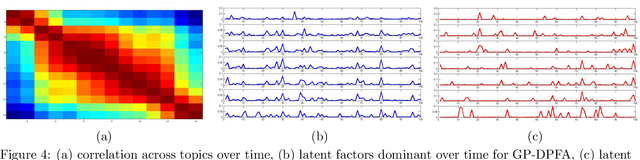

A gamma process dynamic Poisson factor analysis model is proposed to factorize a dynamic count matrix, whose columns are sequentially observed count vectors. The model builds a novel Markov chain that sends the latent gamma random variables at time $(t-1)$ as the shape parameters of those at time $t$, which are linked to observed or latent counts under the Poisson likelihood. The significant challenge of inferring the gamma shape parameters is fully addressed, using unique data augmentation and marginalization techniques for the negative binomial distribution. The same nonparametric Bayesian model also applies to the factorization of a dynamic binary matrix, via a Bernoulli-Poisson link that connects a binary observation to a latent count, with closed-form conditional posteriors for the latent counts and efficient computation for sparse observations. We apply the model to text and music analysis, with state-of-the-art results.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge