Can SGD Select Good Fishermen? Local Convergence under Self-Selection Biases and Beyond
Paper and Code
Apr 06, 2025
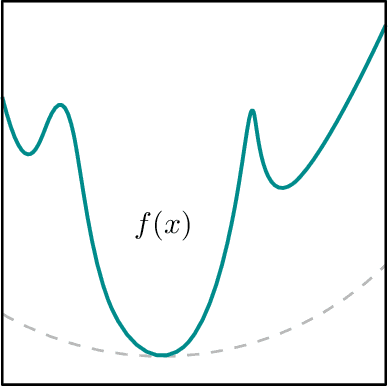
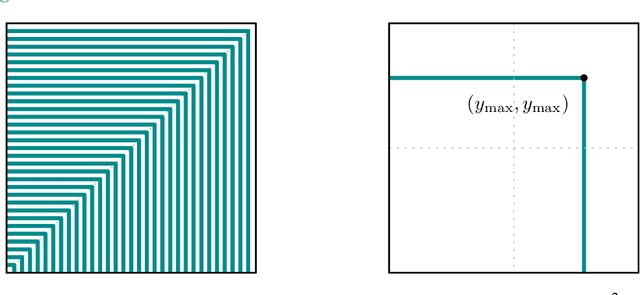
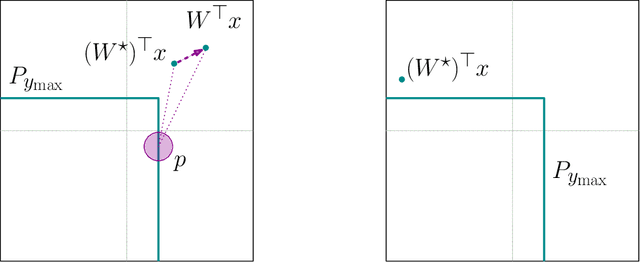
We revisit the problem of estimating $k$ linear regressors with self-selection bias in $d$ dimensions with the maximum selection criterion, as introduced by Cherapanamjeri, Daskalakis, Ilyas, and Zampetakis [CDIZ23, STOC'23]. Our main result is a $\operatorname{poly}(d,k,1/\varepsilon) + {k}^{O(k)}$ time algorithm for this problem, which yields an improvement in the running time of the algorithms of [CDIZ23] and [GM24, arXiv]. We achieve this by providing the first local convergence algorithm for self-selection, thus resolving the main open question of [CDIZ23]. To obtain this algorithm, we reduce self-selection to a seemingly unrelated statistical problem called coarsening. Coarsening occurs when one does not observe the exact value of the sample but only some set (a subset of the sample space) that contains the exact value. Inference from coarse samples arises in various real-world applications due to rounding by humans and algorithms, limited precision of instruments, and lag in multi-agent systems. Our reduction to coarsening is intuitive and relies on the geometry of the self-selection problem, which enables us to bypass the limitations of previous analytic approaches. To demonstrate its applicability, we provide a local convergence algorithm for linear regression under another self-selection criterion, which is related to second-price auction data. Further, we give the first polynomial time local convergence algorithm for coarse Gaussian mean estimation given samples generated from a convex partition. Previously, only a sample-efficient algorithm was known due to Fotakis, Kalavasis, Kontonis, and Tzamos [FKKT21, COLT'21].
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge