Pruning is Optimal for Learning Sparse Features in High-Dimensions

While it is commonly observed in practice that pruning networks to a certain level of sparsity can improve the quality of the features, a theoretical explanation of this phenomenon remains elusive. In this work, we investigate this by demonstrating that a broad class of statistical models can be optimally learned using pruned neural networks trained with gradient descent, in high-dimensions. We consider learning both single-index and multi-index models of the form $y = \sigma^*(\boldsymbol{V}^{\top} \boldsymbol{x}) + \epsilon$, where $\sigma^*$ is a degree-$p$ polynomial, and $\boldsymbol{V} \in \mathbbm{R}^{d \times r}$ with $r \ll d$, is the matrix containing relevant model directions. We assume that $\boldsymbol{V}$ satisfies a certain $\ell_q$-sparsity condition for matrices and show that pruning neural networks proportional to the sparsity level of $\boldsymbol{V}$ improves their sample complexity compared to unpruned networks. Furthermore, we establish Correlational Statistical Query (CSQ) lower bounds in this setting, which take the sparsity level of $\boldsymbol{V}$ into account. We show that if the sparsity level of $\boldsymbol{V}$ exceeds a certain threshold, training pruned networks with a gradient descent algorithm achieves the sample complexity suggested by the CSQ lower bound. In the same scenario, however, our results imply that basis-independent methods such as models trained via standard gradient descent initialized with rotationally invariant random weights can provably achieve only suboptimal sample complexity.

Mirror Descent Strikes Again: Optimal Stochastic Convex Optimization under Infinite Noise Variance

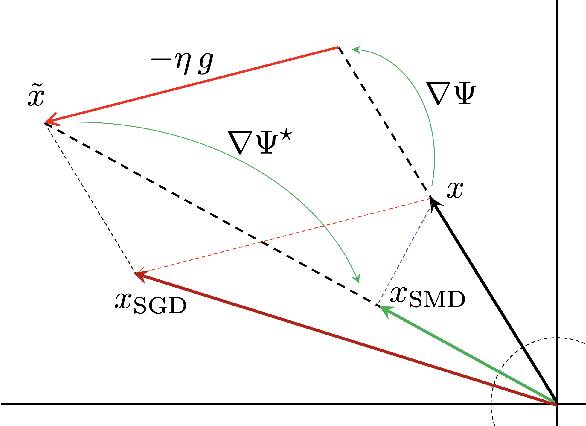
We study stochastic convex optimization under infinite noise variance. Specifically, when the stochastic gradient is unbiased and has uniformly bounded $(1+\kappa)$-th moment, for some $\kappa \in (0,1]$, we quantify the convergence rate of the Stochastic Mirror Descent algorithm with a particular class of uniformly convex mirror maps, in terms of the number of iterations, dimensionality and related geometric parameters of the optimization problem. Interestingly this algorithm does not require any explicit gradient clipping or normalization, which have been extensively used in several recent empirical and theoretical works. We complement our convergence results with information-theoretic lower bounds showing that no other algorithm using only stochastic first-order oracles can achieve improved rates. Our results have several interesting consequences for devising online/streaming stochastic approximation algorithms for problems arising in robust statistics and machine learning.