Optimal Convergence for Stochastic Optimization with Multiple Expectation Constraints
Paper and Code
Jun 15, 2019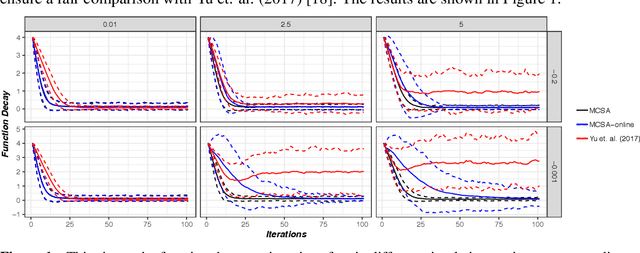
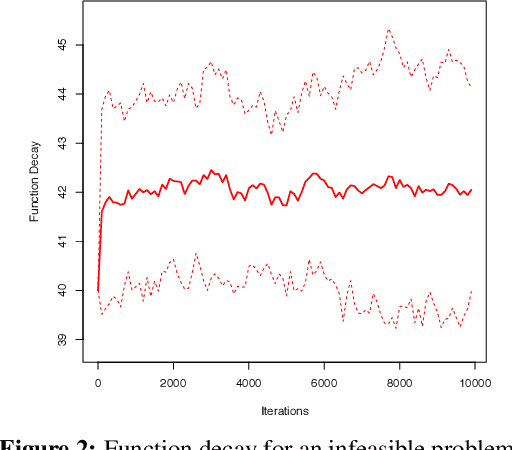
In this paper, we focus on the problem of stochastic optimization where the objective function can be written as an expectation function over a closed convex set. We also consider multiple expectation constraints which restrict the domain of the problem. We extend the cooperative stochastic approximation algorithm from Lan and Zhou [2016] to solve the particular problem. We close the gaps in the previous analysis and provide a novel proof technique to show that our algorithm attains the optimal rate of convergence for both optimality gap and constraint violation when the functions are generally convex. We also compare our algorithm empirically to the state-of-the-art and show improved convergence in many situations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge