Abhishek Chakrabortty
Semi-Supervised Causal Inference: Generalizable and Double Robust Inference for Average Treatment Effects under Selection Bias with Decaying Overlap
May 22, 2023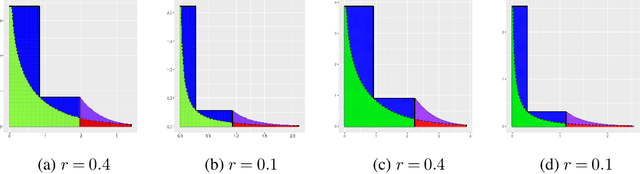
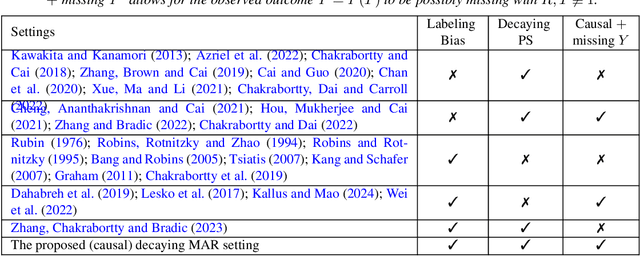
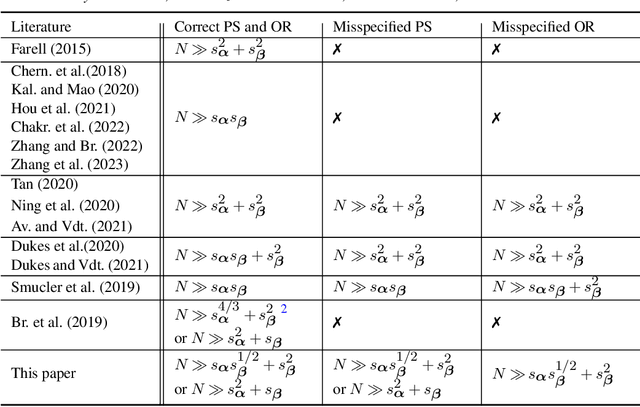
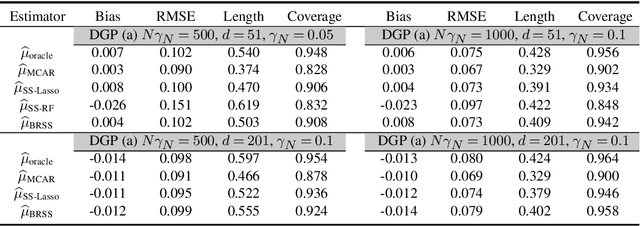
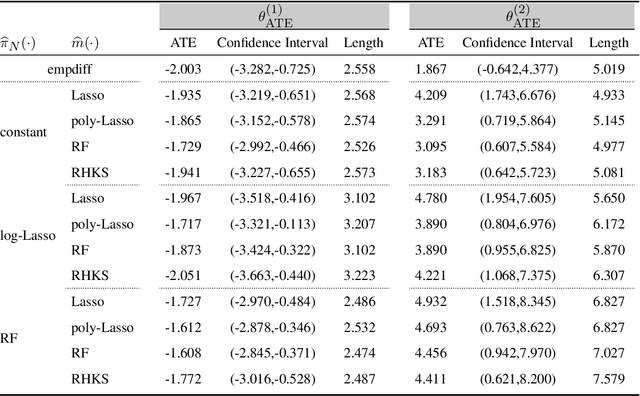
Abstract:Average treatment effect (ATE) estimation is an essential problem in the causal inference literature, which has received significant recent attention, especially with the presence of high-dimensional confounders. We consider the ATE estimation problem in high dimensions when the observed outcome (or label) itself is possibly missing. The labeling indicator's conditional propensity score is allowed to depend on the covariates, and also decay uniformly with sample size - thus allowing for the unlabeled data size to grow faster than the labeled data size. Such a setting fills in an important gap in both the semi-supervised (SS) and missing data literatures. We consider a missing at random (MAR) mechanism that allows selection bias - this is typically forbidden in the standard SS literature, and without a positivity condition - this is typically required in the missing data literature. We first propose a general doubly robust 'decaying' MAR (DR-DMAR) SS estimator for the ATE, which is constructed based on flexible (possibly non-parametric) nuisance estimators. The general DR-DMAR SS estimator is shown to be doubly robust, as well as asymptotically normal (and efficient) when all the nuisance models are correctly specified. Additionally, we propose a bias-reduced DR-DMAR SS estimator based on (parametric) targeted bias-reducing nuisance estimators along with a special asymmetric cross-fitting strategy. We demonstrate that the bias-reduced ATE estimator is asymptotically normal as long as either the outcome regression or the propensity score model is correctly specified. Moreover, the required sparsity conditions are weaker than all the existing doubly robust causal inference literature even under the regular supervised setting - this is a special degenerate case of our setting. Lastly, this work also contributes to the growing literature on generalizability in causal inference.
Semi-Supervised Quantile Estimation: Robust and Efficient Inference in High Dimensional Settings
Jan 25, 2022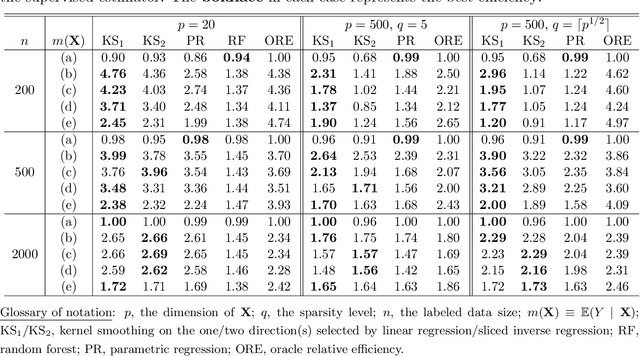
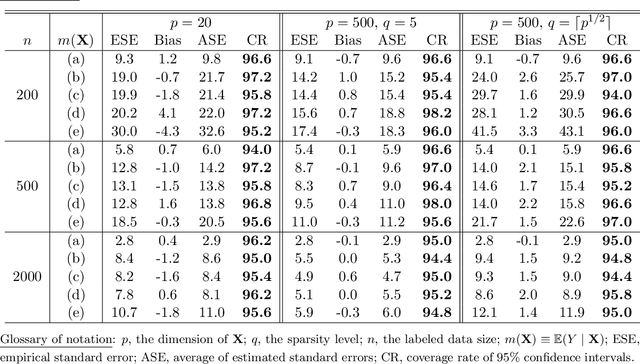
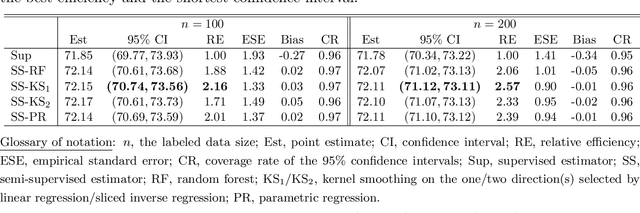
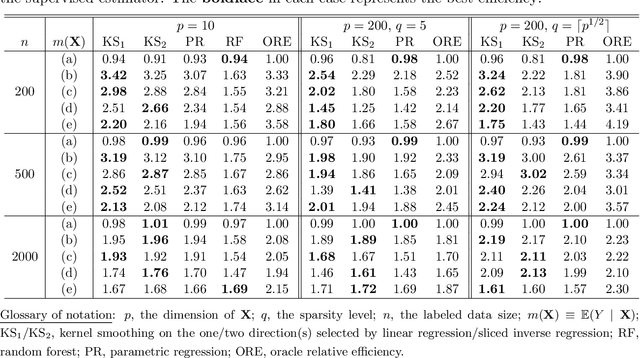
Abstract:We consider quantile estimation in a semi-supervised setting, characterized by two available data sets: (i) a small or moderate sized labeled data set containing observations for a response and a set of possibly high dimensional covariates, and (ii) a much larger unlabeled data set where only the covariates are observed. We propose a family of semi-supervised estimators for the response quantile(s) based on the two data sets, to improve the estimation accuracy compared to the supervised estimator, i.e., the sample quantile from the labeled data. These estimators use a flexible imputation strategy applied to the estimating equation along with a debiasing step that allows for full robustness against misspecification of the imputation model. Further, a one-step update strategy is adopted to enable easy implementation of our method and handle the complexity from the non-linear nature of the quantile estimating equation. Under mild assumptions, our estimators are fully robust to the choice of the nuisance imputation model, in the sense of always maintaining root-n consistency and asymptotic normality, while having improved efficiency relative to the supervised estimator. They also attain semi-parametric optimality if the relation between the response and the covariates is correctly specified via the imputation model. As an illustration of estimating the nuisance imputation function, we consider kernel smoothing type estimators on lower dimensional and possibly estimated transformations of the high dimensional covariates, and we establish novel results on their uniform convergence rates in high dimensions, involving responses indexed by a function class and usage of dimension reduction techniques. These results may be of independent interest. Numerical results on both simulated and real data confirm our semi-supervised approach's improved performance, in terms of both estimation and inference.
A General Framework for Treatment Effect Estimation in Semi-Supervised and High Dimensional Settings
Jan 24, 2022



Abstract:In this article, we aim to provide a general and complete understanding of semi-supervised (SS) causal inference for treatment effects. Specifically, we consider two such estimands: (a) the average treatment effect and (b) the quantile treatment effect, as prototype cases, in an SS setting, characterized by two available data sets: (i) a labeled data set of size $n$, providing observations for a response and a set of high dimensional covariates, as well as a binary treatment indicator; and (ii) an unlabeled data set of size $N$, much larger than $n$, but without the response observed. Using these two data sets, we develop a family of SS estimators which are ensured to be: (1) more robust and (2) more efficient than their supervised counterparts based on the labeled data set only. Beyond the 'standard' double robustness results (in terms of consistency) that can be achieved by supervised methods as well, we further establish root-n consistency and asymptotic normality of our SS estimators whenever the propensity score in the model is correctly specified, without requiring specific forms of the nuisance functions involved. Such an improvement of robustness arises from the use of the massive unlabeled data, so it is generally not attainable in a purely supervised setting. In addition, our estimators are shown to be semi-parametrically efficient as long as all the nuisance functions are correctly specified. Moreover, as an illustration of the nuisance estimators, we consider inverse-probability-weighting type kernel smoothing estimators involving unknown covariate transformation mechanisms, and establish in high dimensional scenarios novel results on their uniform convergence rates, which should be of independent interest. Numerical results on both simulated and real data validate the advantage of our methods over their supervised counterparts with respect to both robustness and efficiency.
Double Robust Semi-Supervised Inference for the Mean: Selection Bias under MAR Labeling with Decaying Overlap
Apr 14, 2021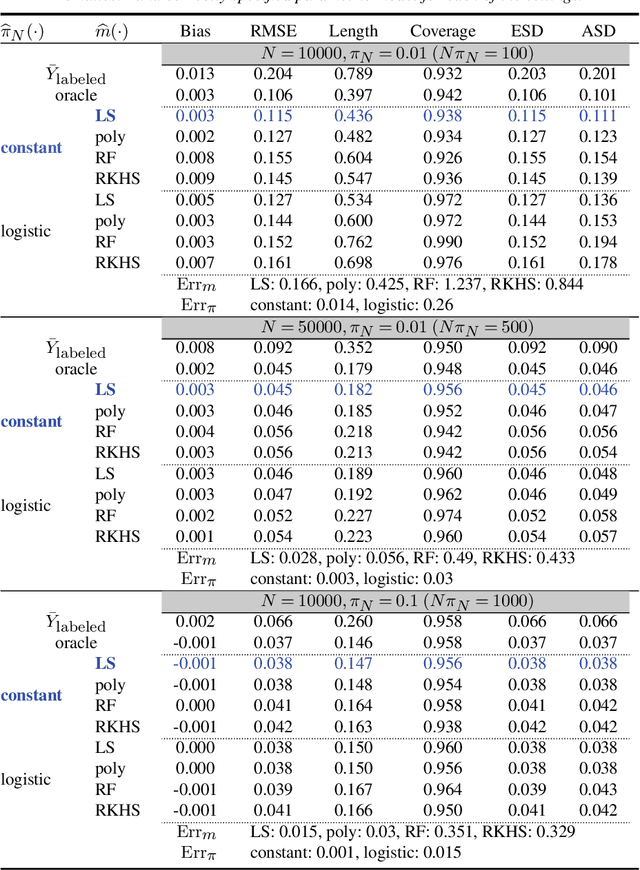
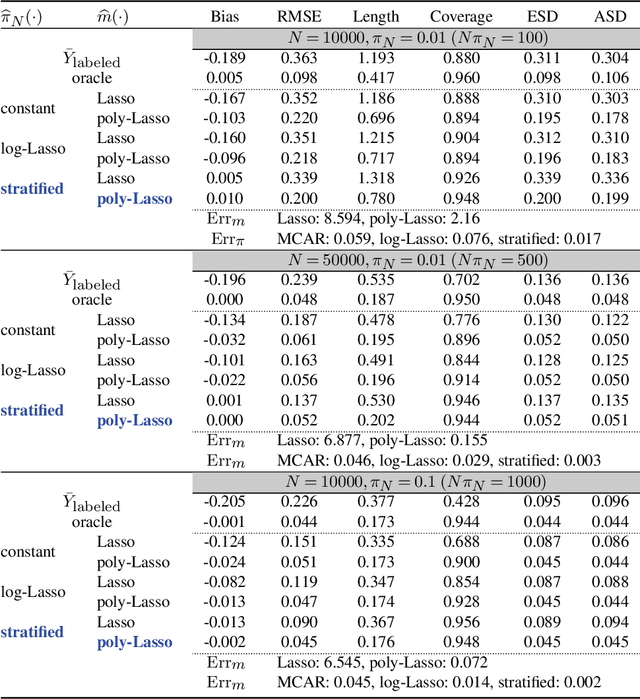
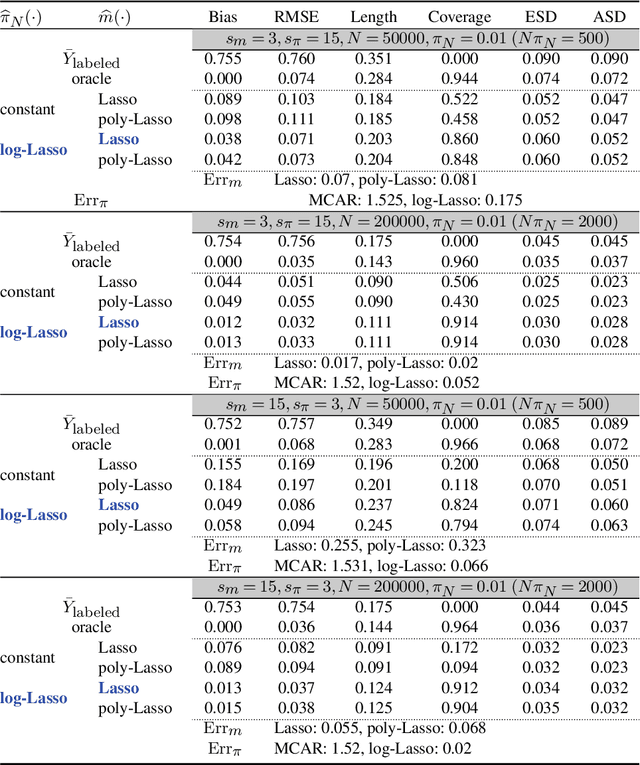
Abstract:Semi-supervised (SS) inference has received much attention in recent years. Apart from a moderate-sized labeled data, L, the SS setting is characterized by an additional, much larger sized, unlabeled data, U. The setting of |U| >> |L|, makes SS inference unique and different from the standard missing data problems, owing to natural violation of the so-called 'positivity' or 'overlap' assumption. However, most of the SS literature implicitly assumes L and U to be equally distributed, i.e., no selection bias in the labeling. Inferential challenges in missing at random (MAR) type labeling allowing for selection bias, are inevitably exacerbated by the decaying nature of the propensity score (PS). We address this gap for a prototype problem, the estimation of the response's mean. We propose a double robust SS (DRSS) mean estimator and give a complete characterization of its asymptotic properties. The proposed estimator is consistent as long as either the outcome or the PS model is correctly specified. When both models are correctly specified, we provide inference results with a non-standard consistency rate that depends on the smaller size |L|. The results are also extended to causal inference with imbalanced treatment groups. Further, we provide several novel choices of models and estimators of the decaying PS, including a novel offset logistic model and a stratified labeling model. We present their properties under both high and low dimensional settings. These may be of independent interest. Lastly, we present extensive simulations and also a real data application.
High Dimensional M-Estimation with Missing Outcomes: A Semi-Parametric Framework
Nov 26, 2019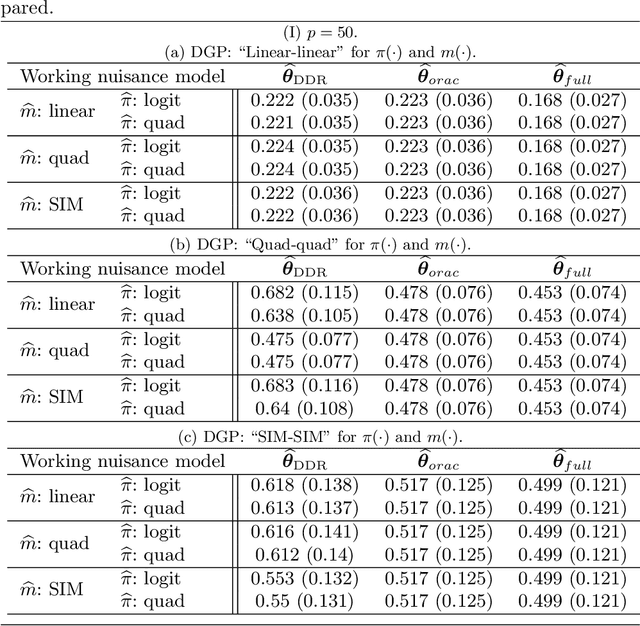
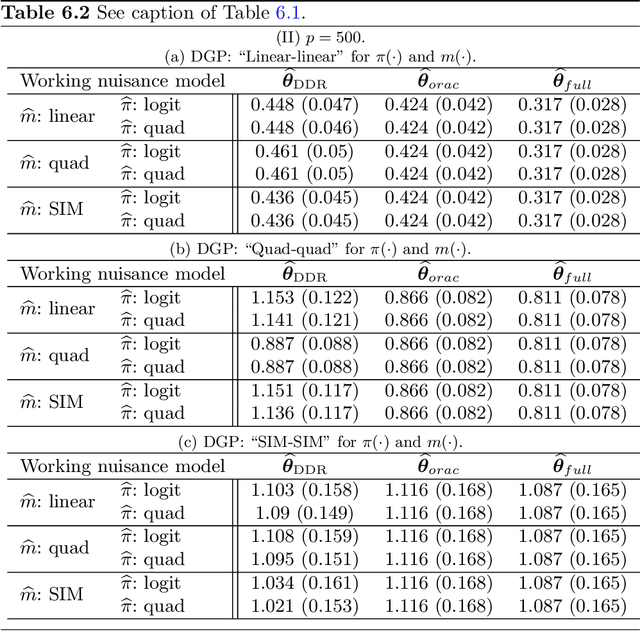
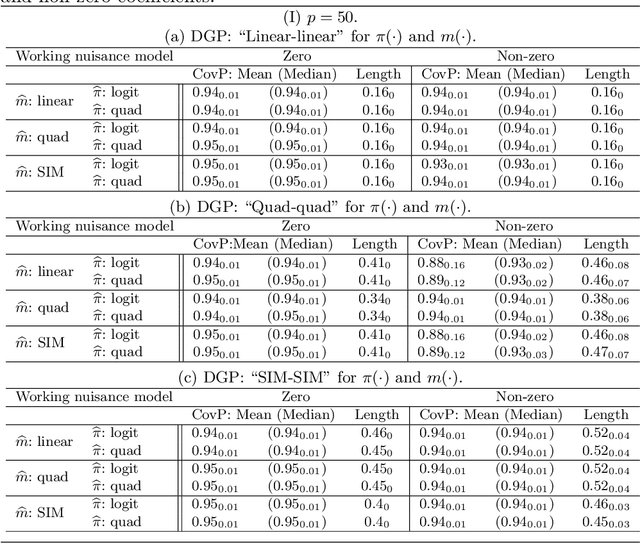
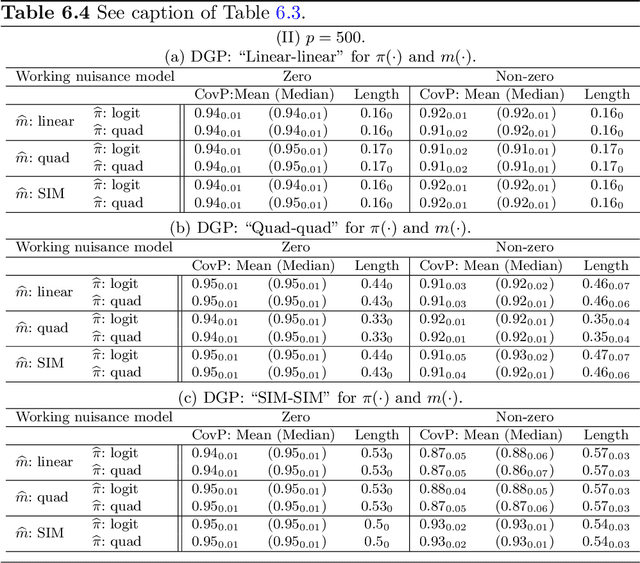
Abstract:We consider high dimensional $M$-estimation in settings where the response $Y$ is possibly missing at random and the covariates $\mathbf{X} \in \mathbb{R}^p$ can be high dimensional compared to the sample size $n$. The parameter of interest $\boldsymbol{\theta}_0 \in \mathbb{R}^d$ is defined as the minimizer of the risk of a convex loss, under a fully non-parametric model, and $\boldsymbol{\theta}_0$ itself is high dimensional which is a key distinction from existing works. Standard high dimensional regression and series estimation with possibly misspecified models and missing $Y$ are included as special cases, as well as their counterparts in causal inference using 'potential outcomes'. Assuming $\boldsymbol{\theta}_0$ is $s$-sparse ($s \ll n$), we propose an $L_1$-regularized debiased and doubly robust (DDR) estimator of $\boldsymbol{\theta}_0$ based on a high dimensional adaptation of the traditional double robust (DR) estimator's construction. Under mild tail assumptions and arbitrarily chosen (working) models for the propensity score (PS) and the outcome regression (OR) estimators, satisfying only some high-level conditions, we establish finite sample performance bounds for the DDR estimator showing its (optimal) $L_2$ error rate to be $\sqrt{s (\log d)/ n}$ when both models are correct, and its consistency and DR properties when only one of them is correct. Further, when both the models are correct, we propose a desparsified version of our DDR estimator that satisfies an asymptotic linear expansion and facilitates inference on low dimensional components of $\boldsymbol{\theta}_0$. Finally, we discuss various of choices of high dimensional parametric/semi-parametric working models for the PS and OR estimators. All results are validated via detailed simulations.
Inference for Individual Mediation Effects and Interventional Effects in Sparse High-Dimensional Causal Graphical Models
Sep 27, 2018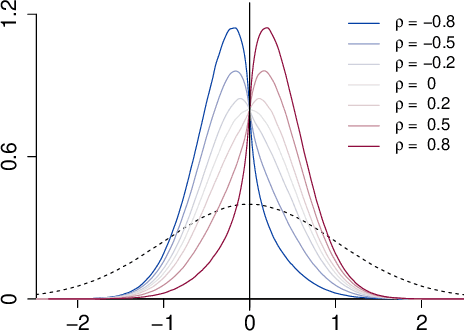
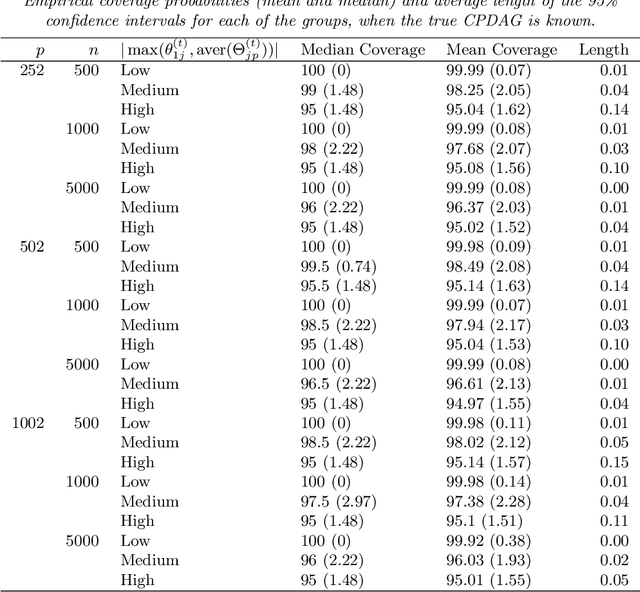
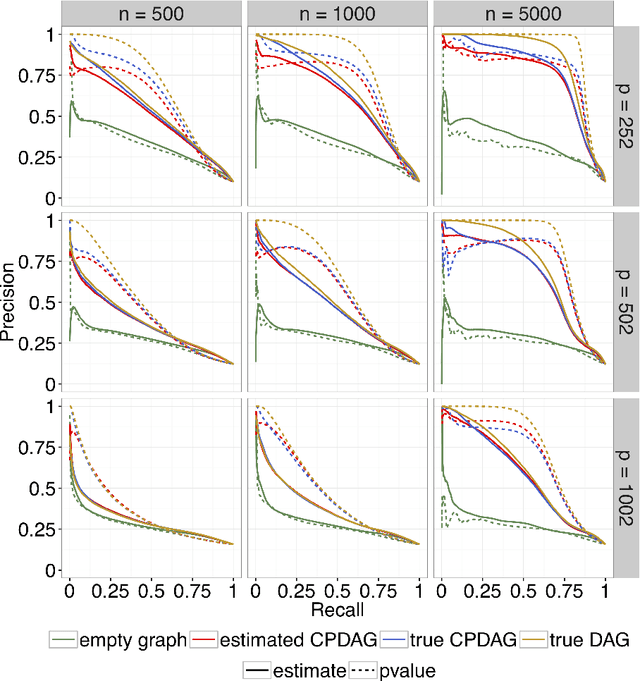
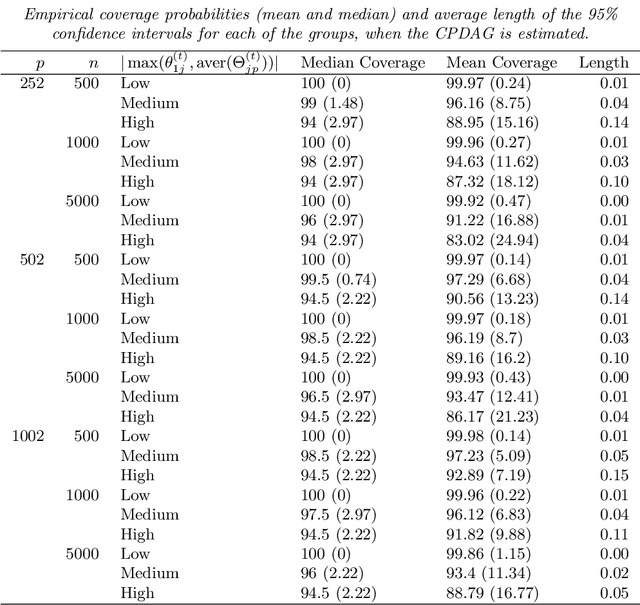
Abstract:We consider the problem of identifying intermediate variables (or mediators) that regulate the effect of a treatment on a response variable. While there has been significant research on this topic, little work has been done when the set of potential mediators is high-dimensional and when they are interrelated. In particular, we assume that the causal structure of the treatment, the potential mediators and the response is a directed acyclic graph (DAG). High-dimensional DAG models have previously been used for the estimation of causal effects from observational data and methods called IDA and joint-IDA have been developed for estimating the effects of single interventions and multiple simultaneous interventions respectively. In this paper, we propose an IDA-type method called MIDA for estimating mediation effects from high-dimensional observational data. Although IDA and joint-IDA estimators have been shown to be consistent in certain sparse high-dimensional settings, their asymptotic properties such as convergence in distribution and inferential tools in such settings remained unknown. We prove high-dimensional consistency of MIDA for linear structural equation models with sub-Gaussian errors. More importantly, we derive distributional convergence results for MIDA in similar high-dimensional settings, which are applicable to IDA and joint-IDA estimators as well. To the best of our knowledge, these are the first distributional convergence results facilitating inference for IDA-type estimators. These results have been built on our novel theoretical results regarding uniform bounds for linear regression estimators over varying subsets of high-dimensional covariates, which may be of independent interest. Finally, we empirically validate our asymptotic theory and demonstrate the usefulness of MIDA in identifying large mediation effects via simulations and application to real data in genomics.
Surrogate Aided Unsupervised Recovery of Sparse Signals in Single Index Models for Binary Outcomes
Jul 01, 2018



Abstract:We consider the recovery of regression coefficients, denoted by $\boldsymbol{\beta}_0$, for a single index model (SIM) relating a binary outcome $Y$ to a set of possibly high dimensional covariates $\boldsymbol{X}$, based on a large but 'unlabeled' dataset $\mathcal{U}$, with $Y$ never observed. On $\mathcal{U}$, we fully observe $\boldsymbol{X}$ and additionally, a surrogate $S$ which, while not being strongly predictive of $Y$ throughout the entirety of its support, can forecast it with high accuracy when it assumes extreme values. Such datasets arise naturally in modern studies involving large databases such as electronic medical records (EMR) where $Y$, unlike $(\boldsymbol{X}, S)$, is difficult and/or expensive to obtain. In EMR studies, an example of $Y$ and $S$ would be the true disease phenotype and the count of the associated diagnostic codes respectively. Assuming another SIM for $S$ given $\boldsymbol{X}$, we show that under sparsity assumptions, we can recover $\boldsymbol{\beta}_0$ proportionally by simply fitting a least squares LASSO estimator to the subset of the observed data on $(\boldsymbol{X}, S)$ restricted to the extreme sets of $S$, with $Y$ imputed using the surrogacy of $S$. We obtain sharp finite sample performance bounds for our estimator, including deterministic deviation bounds and probabilistic guarantees. We demonstrate the effectiveness of our approach through multiple simulation studies, as well as by application to real data from an EMR study conducted at the Partners HealthCare Systems.
Moving Beyond Sub-Gaussianity in High-Dimensional Statistics: Applications in Covariance Estimation and Linear Regression
Jun 29, 2018Abstract:Concentration inequalities form an essential toolkit in the study of high-dimensional statistical methods. Most of the relevant statistics literature is based on the assumptions of sub-Gaussian/sub-exponential random vectors. In this paper, we bring together various probability inequalities for sums of independent random variables under much weaker exponential type (sub-Weibull) tail assumptions. These results extract a part sub-Gaussian tail behavior in finite samples, matching the asymptotics governed by the central limit theorem, and are compactly represented in terms of a new Orlicz quasi-norm - the Generalized Bernstein-Orlicz norm - that typifies such tail behaviors. We illustrate the usefulness of these inequalities through the analysis of four fundamental problems in high-dimensional statistics. In the first two problems, we study the rate of convergence of the sample covariance matrix in terms of the maximum elementwise norm and the maximum k-sub-matrix operator norm which are key quantities of interest in bootstrap procedures and high-dimensional structured covariance matrix estimation. The third example concerns the restricted eigenvalue condition, required in high dimensional linear regression, which we verify for all sub-Weibull random vectors under only marginal (not joint) tail assumptions on the covariates. To our knowledge, this is the first unified result obtained in such generality. In the final example, we consider the Lasso estimator for linear regression and establish its rate of convergence under much weaker tail assumptions (on the errors as well as the covariates) than those in the existing literature. The common feature in all our results is that the convergence rates under most exponential tails match the usual ones under sub-Gaussian assumptions. Finally, we also establish a high-dimensional CLT and tail bounds for empirical processes for sub-Weibulls.
Efficient and Adaptive Linear Regression in Semi-Supervised Settings
Aug 19, 2017



Abstract:We consider the linear regression problem under semi-supervised settings wherein the available data typically consists of: (i) a small or moderate sized 'labeled' data, and (ii) a much larger sized 'unlabeled' data. Such data arises naturally from settings where the outcome, unlike the covariates, is expensive to obtain, a frequent scenario in modern studies involving large databases like electronic medical records (EMR). Supervised estimators like the ordinary least squares (OLS) estimator utilize only the labeled data. It is often of interest to investigate if and when the unlabeled data can be exploited to improve estimation of the regression parameter in the adopted linear model. In this paper, we propose a class of 'Efficient and Adaptive Semi-Supervised Estimators' (EASE) to improve estimation efficiency. The EASE are two-step estimators adaptive to model mis-specification, leading to improved (optimal in some cases) efficiency under model mis-specification, and equal (optimal) efficiency under a linear model. This adaptive property, often unaddressed in the existing literature, is crucial for advocating 'safe' use of the unlabeled data. The construction of EASE primarily involves a flexible 'semi-non-parametric' imputation, including a smoothing step that works well even when the number of covariates is not small; and a follow up 'refitting' step along with a cross-validation (CV) strategy both of which have useful practical as well as theoretical implications towards addressing two important issues: under-smoothing and over-fitting. We establish asymptotic results including consistency, asymptotic normality and the adaptive properties of EASE. We also provide influence function expansions and a 'double' CV strategy for inference. The results are further validated through extensive simulations, followed by application to an EMR study on auto-immunity.
* 51 pages; Revised version - to appear in The Annals of Statistics
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge