Semi-Supervised Causal Inference: Generalizable and Double Robust Inference for Average Treatment Effects under Selection Bias with Decaying Overlap

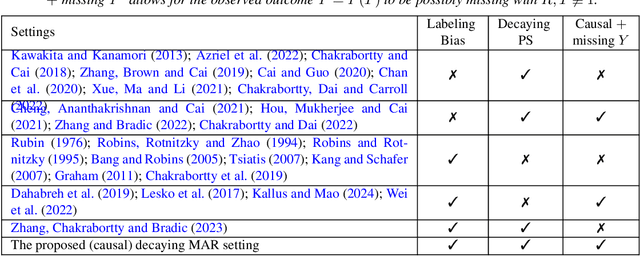
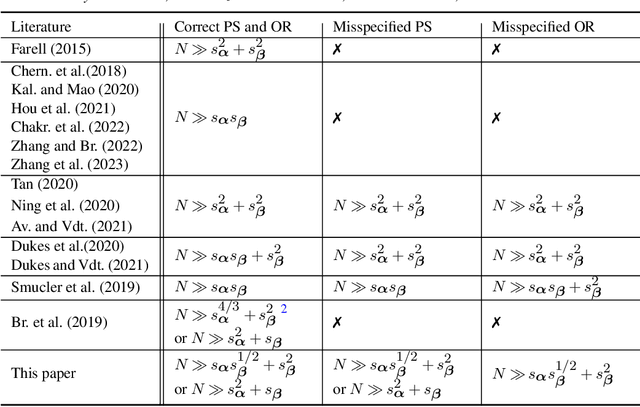
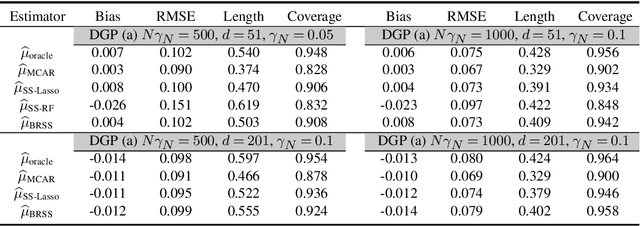
Average treatment effect (ATE) estimation is an essential problem in the causal inference literature, which has received significant recent attention, especially with the presence of high-dimensional confounders. We consider the ATE estimation problem in high dimensions when the observed outcome (or label) itself is possibly missing. The labeling indicator's conditional propensity score is allowed to depend on the covariates, and also decay uniformly with sample size - thus allowing for the unlabeled data size to grow faster than the labeled data size. Such a setting fills in an important gap in both the semi-supervised (SS) and missing data literatures. We consider a missing at random (MAR) mechanism that allows selection bias - this is typically forbidden in the standard SS literature, and without a positivity condition - this is typically required in the missing data literature. We first propose a general doubly robust 'decaying' MAR (DR-DMAR) SS estimator for the ATE, which is constructed based on flexible (possibly non-parametric) nuisance estimators. The general DR-DMAR SS estimator is shown to be doubly robust, as well as asymptotically normal (and efficient) when all the nuisance models are correctly specified. Additionally, we propose a bias-reduced DR-DMAR SS estimator based on (parametric) targeted bias-reducing nuisance estimators along with a special asymmetric cross-fitting strategy. We demonstrate that the bias-reduced ATE estimator is asymptotically normal as long as either the outcome regression or the propensity score model is correctly specified. Moreover, the required sparsity conditions are weaker than all the existing doubly robust causal inference literature even under the regular supervised setting - this is a special degenerate case of our setting. Lastly, this work also contributes to the growing literature on generalizability in causal inference.