High Dimensional M-Estimation with Missing Outcomes: A Semi-Parametric Framework
Paper and Code
Nov 26, 2019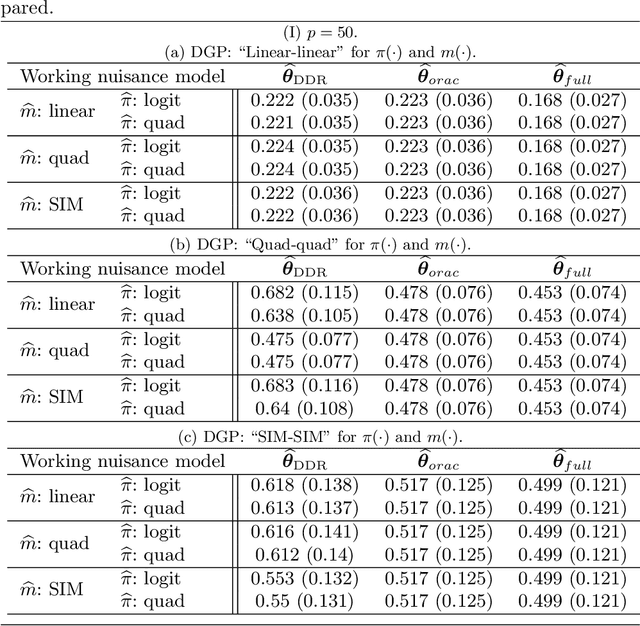
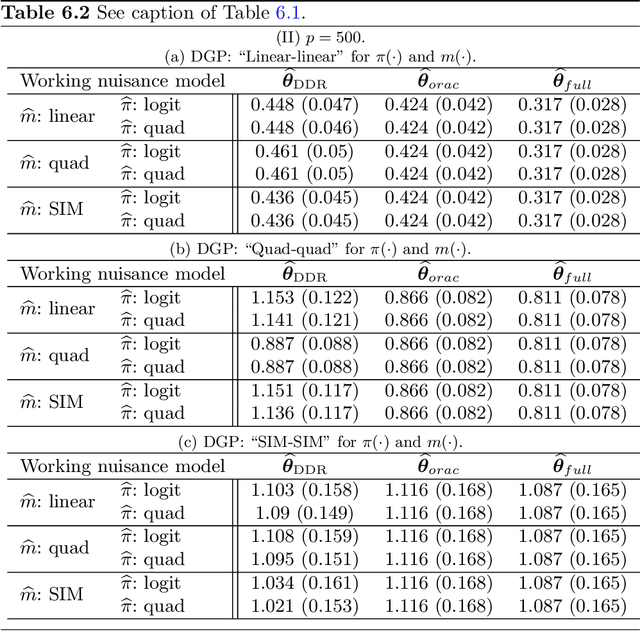
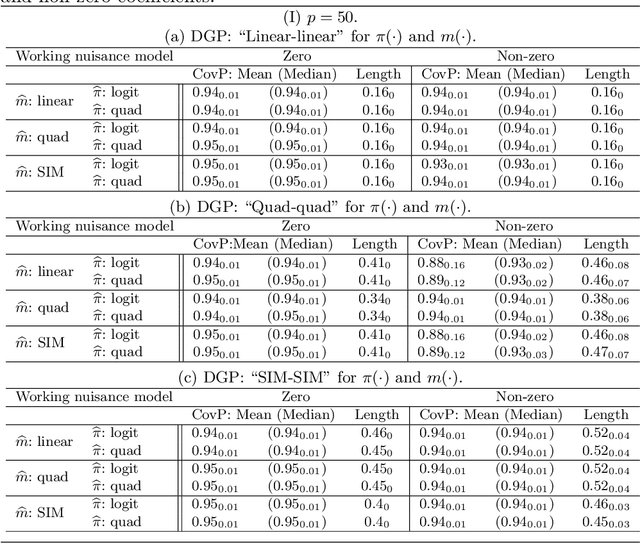
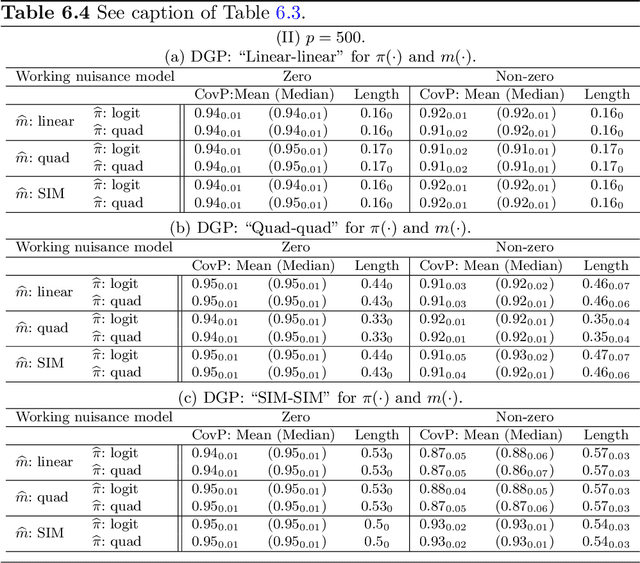
We consider high dimensional $M$-estimation in settings where the response $Y$ is possibly missing at random and the covariates $\mathbf{X} \in \mathbb{R}^p$ can be high dimensional compared to the sample size $n$. The parameter of interest $\boldsymbol{\theta}_0 \in \mathbb{R}^d$ is defined as the minimizer of the risk of a convex loss, under a fully non-parametric model, and $\boldsymbol{\theta}_0$ itself is high dimensional which is a key distinction from existing works. Standard high dimensional regression and series estimation with possibly misspecified models and missing $Y$ are included as special cases, as well as their counterparts in causal inference using 'potential outcomes'. Assuming $\boldsymbol{\theta}_0$ is $s$-sparse ($s \ll n$), we propose an $L_1$-regularized debiased and doubly robust (DDR) estimator of $\boldsymbol{\theta}_0$ based on a high dimensional adaptation of the traditional double robust (DR) estimator's construction. Under mild tail assumptions and arbitrarily chosen (working) models for the propensity score (PS) and the outcome regression (OR) estimators, satisfying only some high-level conditions, we establish finite sample performance bounds for the DDR estimator showing its (optimal) $L_2$ error rate to be $\sqrt{s (\log d)/ n}$ when both models are correct, and its consistency and DR properties when only one of them is correct. Further, when both the models are correct, we propose a desparsified version of our DDR estimator that satisfies an asymptotic linear expansion and facilitates inference on low dimensional components of $\boldsymbol{\theta}_0$. Finally, we discuss various of choices of high dimensional parametric/semi-parametric working models for the PS and OR estimators. All results are validated via detailed simulations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge