Doubly High-Dimensional Contextual Bandits: An Interpretable Model for Joint Assortment-Pricing

Key challenges in running a retail business include how to select products to present to consumers (the assortment problem), and how to price products (the pricing problem) to maximize revenue or profit. Instead of considering these problems in isolation, we propose a joint approach to assortment-pricing based on contextual bandits. Our model is doubly high-dimensional, in that both context vectors and actions are allowed to take values in high-dimensional spaces. In order to circumvent the curse of dimensionality, we propose a simple yet flexible model that captures the interactions between covariates and actions via a (near) low-rank representation matrix. The resulting class of models is reasonably expressive while remaining interpretable through latent factors, and includes various structured linear bandit and pricing models as particular cases. We propose a computationally tractable procedure that combines an exploration/exploitation protocol with an efficient low-rank matrix estimator, and we prove bounds on its regret. Simulation results show that this method has lower regret than state-of-the-art methods applied to various standard bandit and pricing models. Real-world case studies on the assortment-pricing problem, from an industry-leading instant noodles company to an emerging beauty start-up, underscore the gains achievable using our method. In each case, we show at least three-fold gains in revenue or profit by our bandit method, as well as the interpretability of the latent factor models that are learned.

Nonparametric Empirical Bayes Estimation and Testing for Sparse and Heteroscedastic Signals

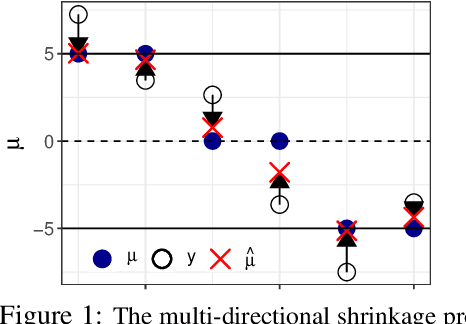
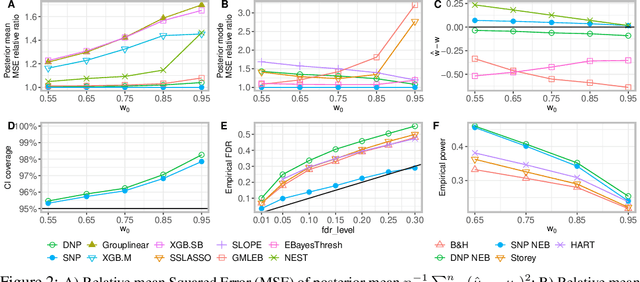
Large-scale modern data often involves estimation and testing for high-dimensional unknown parameters. It is desirable to identify the sparse signals, ``the needles in the haystack'', with accuracy and false discovery control. However, the unprecedented complexity and heterogeneity in modern data structure require new machine learning tools to effectively exploit commonalities and to robustly adjust for both sparsity and heterogeneity. In addition, estimates for high-dimensional parameters often lack uncertainty quantification. In this paper, we propose a novel Spike-and-Nonparametric mixture prior (SNP) -- a spike to promote the sparsity and a nonparametric structure to capture signals. In contrast to the state-of-the-art methods, the proposed methods solve the estimation and testing problem at once with several merits: 1) an accurate sparsity estimation; 2) point estimates with shrinkage/soft-thresholding property; 3) credible intervals for uncertainty quantification; 4) an optimal multiple testing procedure that controls false discovery rate. Our method exhibits promising empirical performance on both simulated data and a gene expression case study.