Differentially Private Conditional Independence Testing

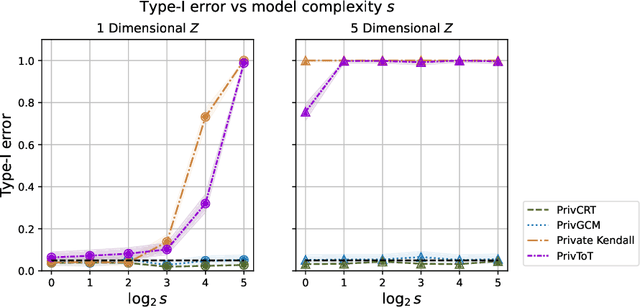
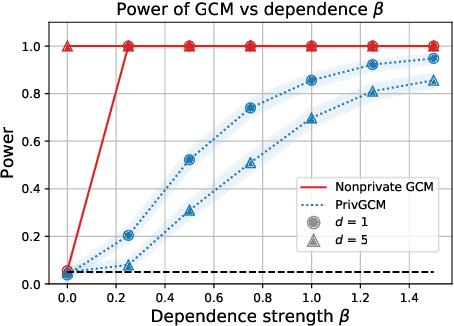
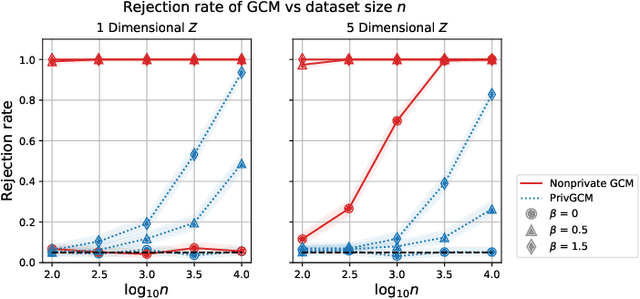
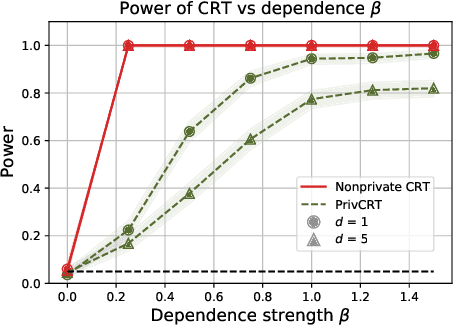
Conditional independence (CI) tests are widely used in statistical data analysis, e.g., they are the building block of many algorithms for causal graph discovery. The goal of a CI test is to accept or reject the null hypothesis that $X \perp \!\!\! \perp Y \mid Z$, where $X \in \mathbb{R}, Y \in \mathbb{R}, Z \in \mathbb{R}^d$. In this work, we investigate conditional independence testing under the constraint of differential privacy. We design two private CI testing procedures: one based on the generalized covariance measure of Shah and Peters (2020) and another based on the conditional randomization test of Cand\`es et al. (2016) (under the model-X assumption). We provide theoretical guarantees on the performance of our tests and validate them empirically. These are the first private CI tests that work for the general case when $Z$ is continuous.

Performative Prediction in a Stateful World

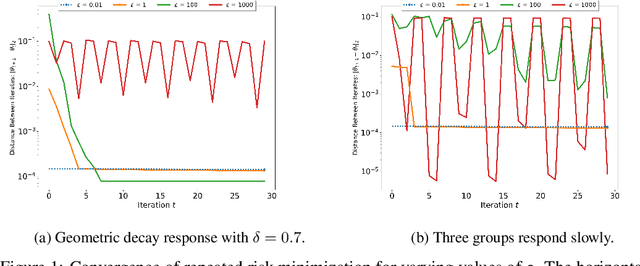
Deployed supervised machine learning models make predictions that interact with and influence the world. This phenomenon is called "performative prediction" by Perdomo et al. (2020), who investigated it in a stateless setting. We generalize their results to the case where the response of the population to the deployed classifier depends both on the classifier and the previous distribution of the population. We also demonstrate such a setting empirically, for the scenario of strategic manipulation.