Differentially Private Conditional Independence Testing
Paper and Code
Jun 11, 2023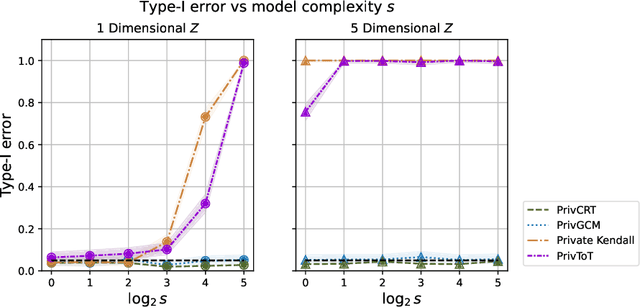
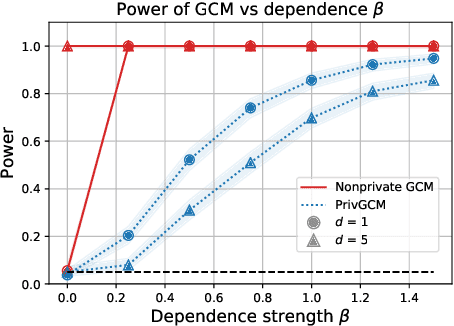
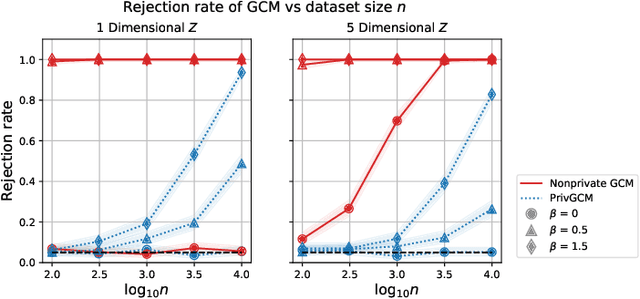
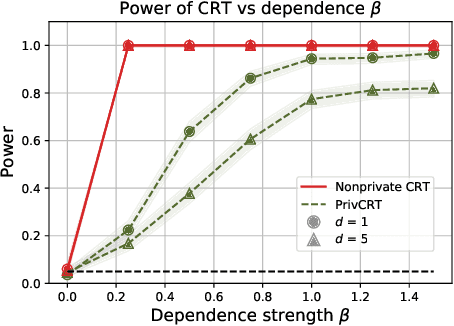
Conditional independence (CI) tests are widely used in statistical data analysis, e.g., they are the building block of many algorithms for causal graph discovery. The goal of a CI test is to accept or reject the null hypothesis that $X \perp \!\!\! \perp Y \mid Z$, where $X \in \mathbb{R}, Y \in \mathbb{R}, Z \in \mathbb{R}^d$. In this work, we investigate conditional independence testing under the constraint of differential privacy. We design two private CI testing procedures: one based on the generalized covariance measure of Shah and Peters (2020) and another based on the conditional randomization test of Cand\`es et al. (2016) (under the model-X assumption). We provide theoretical guarantees on the performance of our tests and validate them empirically. These are the first private CI tests that work for the general case when $Z$ is continuous.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge