Inferring Kernel $ε$-Machines: Discovering Structure in Complex Systems

Previously, we showed that computational mechanic's causal states -- predictively-equivalent trajectory classes for a stochastic dynamical system -- can be cast into a reproducing kernel Hilbert space. The result is a widely-applicable method that infers causal structure directly from very different kinds of observations and systems. Here, we expand this method to explicitly introduce the causal diffusion components it produces. These encode the kernel causal-state estimates as a set of coordinates in a reduced dimension space. We show how each component extracts predictive features from data and demonstrate their application on four examples: first, a simple pendulum -- an exactly solvable system; second, a molecular-dynamic trajectory of $n$-butane -- a high-dimensional system with a well-studied energy landscape; third, the monthly sunspot sequence -- the longest-running available time series of direct observations; and fourth, multi-year observations of an active crop field -- a set of heterogeneous observations of the same ecosystem taken for over a decade. In this way, we demonstrate that the empirical kernel causal-states algorithm robustly discovers predictive structures for systems with widely varying dimensionality and stochasticity.

Discovering Causal Structure with Reproducing-Kernel Hilbert Space $ε$-Machines

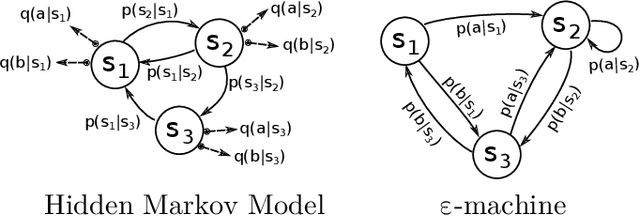
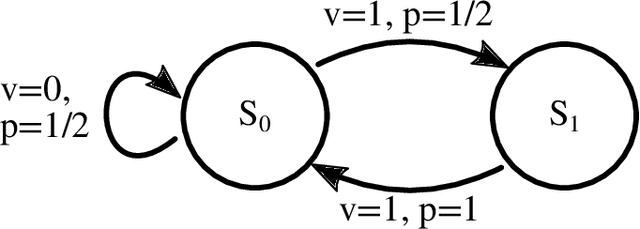
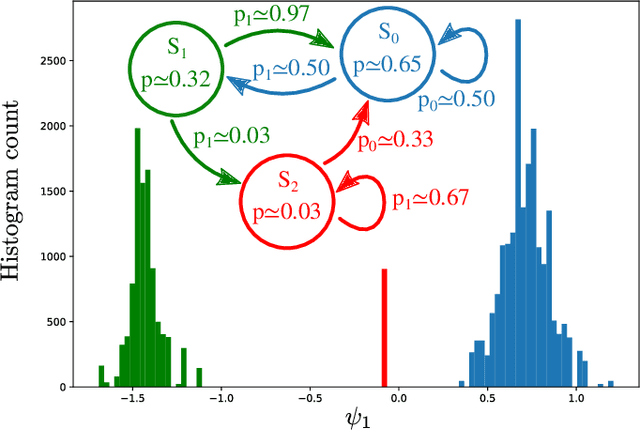
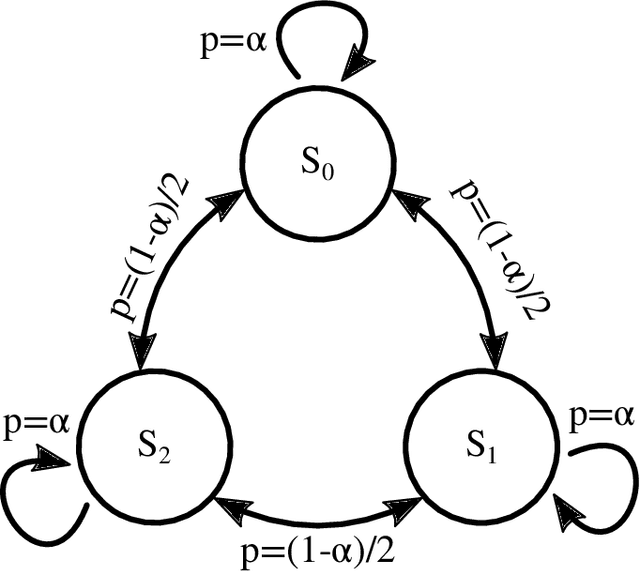
We merge computational mechanics' definition of causal states (predictively-equivalent histories) with reproducing-kernel Hilbert space (RKHS) representation inference. The result is a widely-applicable method that infers causal structure directly from observations of a system's behaviors whether they are over discrete or continuous events or time. A structural representation -- a finite- or infinite-state kernel $\epsilon$-machine -- is extracted by a reduced-dimension transform that gives an efficient representation of causal states and their topology. In this way, the system dynamics are represented by a stochastic (ordinary or partial) differential equation that acts on causal states. We introduce an algorithm to estimate the associated evolution operator. Paralleling the Fokker-Plank equation, it efficiently evolves causal-state distributions and makes predictions in the original data space via an RKHS functional mapping. We demonstrate these techniques, together with their predictive abilities, on discrete-time, discrete-value infinite Markov-order processes generated by finite-state hidden Markov models with (i) finite or (ii) uncountably-infinite causal states and (iii) a continuous-time, continuous-value process generated by a thermally-driven chaotic flow. The method robustly estimates causal structure in the presence of varying external and measurement noise levels.

Super-resolving multiresolution images with band-independant geometry of multispectral pixels

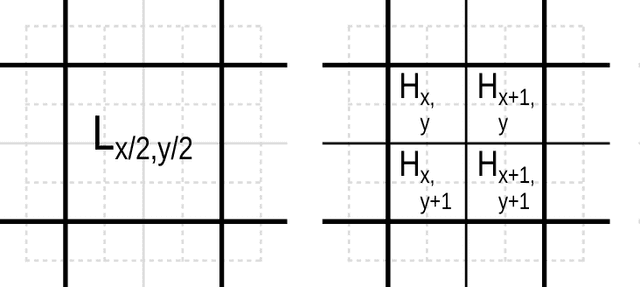
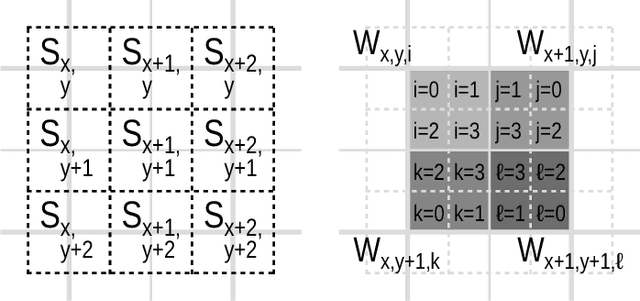
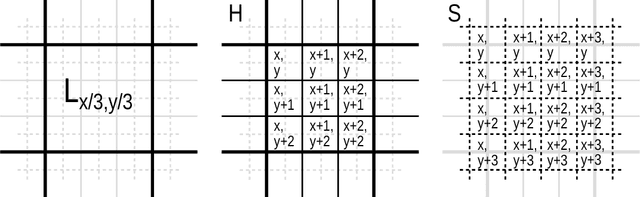
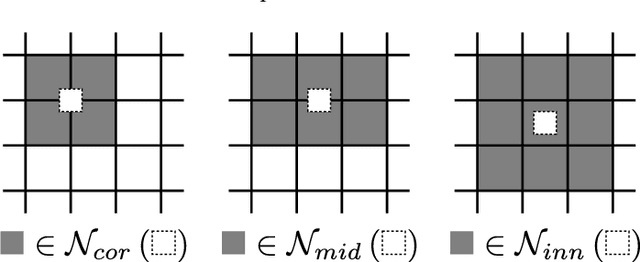
A new resolution enhancement method is presented for multispectral and multi-resolution images, such as these provided by the Sentinel-2 satellites. Starting from the highest resolution bands, band-dependent information (reflectance) is separated from information that is common to all bands (geometry of scene elements). This model is then applied to unmix low-resolution bands, preserving their reflectance, while propagating band-independent information to preserve the sub-pixel details. A reference implementation is provided, with an application example for super-resolving Sentinel-2 data.

Stochastic Texture Difference for Scale-Dependent Data Analysis

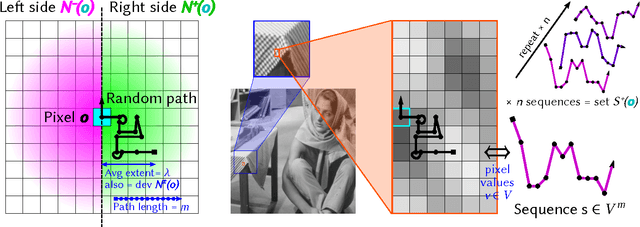
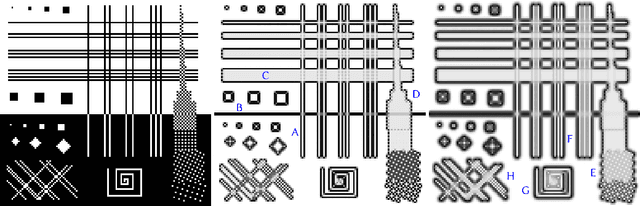
This article introduces the Stochastic Texture Difference method for analyzing data at prescribed spatial and value scales. This method relies on constrained random walks around each pixel, describing how nearby image values typically evolve on each side of this pixel. Textures are represented as probability distributions of such random walks, so a texture difference operator is statistically defined as a distance between these distributions in a suitable reproducing kernel Hilbert space. The method is thus not limited to scalar pixel values: any data type for which a kernel is available may be considered, from color triplets and multispectral vector data to strings, graphs, and more. By adjusting the size of the neighborhoods that are compared, the method is implicitly scale-dependent. It is also able to focus on either small changes or large gradients. We demonstrate how it can be used to infer spatial and data value characteristic scales in measured signals and natural images.

3D Terrestrial lidar data classification of complex natural scenes using a multi-scale dimensionality criterion: applications in geomorphology

3D point clouds of natural environments relevant to problems in geomorphology often require classification of the data into elementary relevant classes. A typical example is the separation of riparian vegetation from ground in fluvial environments, the distinction between fresh surfaces and rockfall in cliff environments, or more generally the classification of surfaces according to their morphology. Natural surfaces are heterogeneous and their distinctive properties are seldom defined at a unique scale, prompting the use of multi-scale criteria to achieve a high degree of classification success. We have thus defined a multi-scale measure of the point cloud dimensionality around each point, which characterizes the local 3D organization. We can thus monitor how the local cloud geometry behaves across scales. We present the technique and illustrate its efficiency in separating riparian vegetation from ground and classifying a mountain stream as vegetation, rock, gravel or water surface. In these two cases, separating the vegetation from ground or other classes achieve accuracy larger than 98 %. Comparison with a single scale approach shows the superiority of the multi-scale analysis in enhancing class separability and spatial resolution. The technique is robust to missing data, shadow zones and changes in point density within the scene. The classification is fast and accurate and can account for some degree of intra-class morphological variability such as different vegetation types. A probabilistic confidence in the classification result is given at each point, allowing the user to remove the points for which the classification is uncertain. The process can be both fully automated, but also fully customized by the user including a graphical definition of the classifiers. Although developed for fully 3D data, the method can be readily applied to 2.5D airborne lidar data.

Reconstruction of Epsilon-Machines in Predictive Frameworks and Decisional States

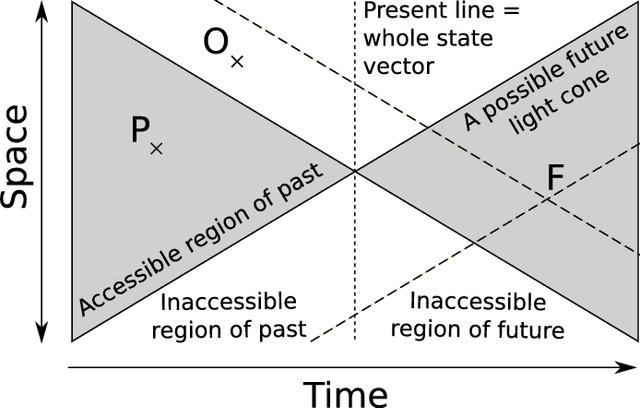
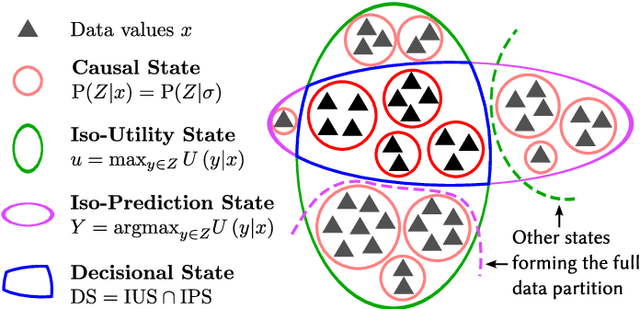
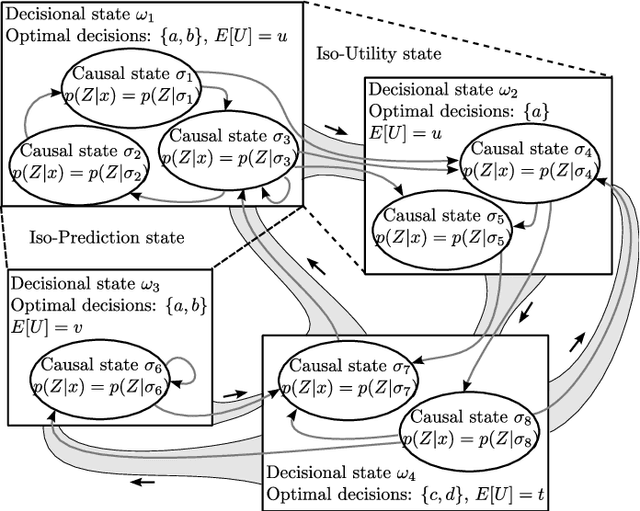
This article introduces both a new algorithm for reconstructing epsilon-machines from data, as well as the decisional states. These are defined as the internal states of a system that lead to the same decision, based on a user-provided utility or pay-off function. The utility function encodes some a priori knowledge external to the system, it quantifies how bad it is to make mistakes. The intrinsic underlying structure of the system is modeled by an epsilon-machine and its causal states. The decisional states form a partition of the lower-level causal states that is defined according to the higher-level user's knowledge. In a complex systems perspective, the decisional states are thus the "emerging" patterns corresponding to the utility function. The transitions between these decisional states correspond to events that lead to a change of decision. The new REMAPF algorithm estimates both the epsilon-machine and the decisional states from data. Application examples are given for hidden model reconstruction, cellular automata filtering, and edge detection in images.