Hussein Yahia
Stochastic Texture Difference for Scale-Dependent Data Analysis
Oct 05, 2015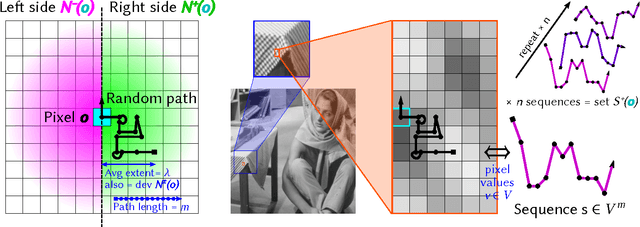
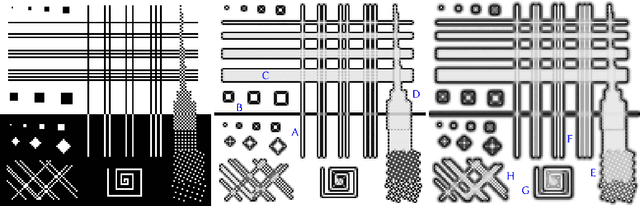


Abstract:This article introduces the Stochastic Texture Difference method for analyzing data at prescribed spatial and value scales. This method relies on constrained random walks around each pixel, describing how nearby image values typically evolve on each side of this pixel. Textures are represented as probability distributions of such random walks, so a texture difference operator is statistically defined as a distance between these distributions in a suitable reproducing kernel Hilbert space. The method is thus not limited to scalar pixel values: any data type for which a kernel is available may be considered, from color triplets and multispectral vector data to strings, graphs, and more. By adjusting the size of the neighborhoods that are compared, the method is implicitly scale-dependent. It is also able to focus on either small changes or large gradients. We demonstrate how it can be used to infer spatial and data value characteristic scales in measured signals and natural images.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge