Inferring Kernel $ε$-Machines: Discovering Structure in Complex Systems

Previously, we showed that computational mechanic's causal states -- predictively-equivalent trajectory classes for a stochastic dynamical system -- can be cast into a reproducing kernel Hilbert space. The result is a widely-applicable method that infers causal structure directly from very different kinds of observations and systems. Here, we expand this method to explicitly introduce the causal diffusion components it produces. These encode the kernel causal-state estimates as a set of coordinates in a reduced dimension space. We show how each component extracts predictive features from data and demonstrate their application on four examples: first, a simple pendulum -- an exactly solvable system; second, a molecular-dynamic trajectory of $n$-butane -- a high-dimensional system with a well-studied energy landscape; third, the monthly sunspot sequence -- the longest-running available time series of direct observations; and fourth, multi-year observations of an active crop field -- a set of heterogeneous observations of the same ecosystem taken for over a decade. In this way, we demonstrate that the empirical kernel causal-states algorithm robustly discovers predictive structures for systems with widely varying dimensionality and stochasticity.

Shannon Entropy Rate of Hidden Markov Processes

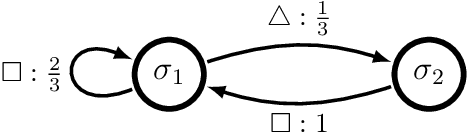
Hidden Markov chains are widely applied statistical models of stochastic processes, from fundamental physics and chemistry to finance, health, and artificial intelligence. The hidden Markov processes they generate are notoriously complicated, however, even if the chain is finite state: no finite expression for their Shannon entropy rate exists, as the set of their predictive features is generically infinite. As such, to date one cannot make general statements about how random they are nor how structured. Here, we address the first part of this challenge by showing how to efficiently and accurately calculate their entropy rates. We also show how this method gives the minimal set of infinite predictive features. A sequel addresses the challenge's second part on structure.