Tune As You Scale: Hyperparameter Optimization For Compute Efficient Training

Hyperparameter tuning of deep learning models can lead to order-of-magnitude performance gains for the same amount of compute. Despite this, systematic tuning is uncommon, particularly for large models, which are expensive to evaluate and tend to have many hyperparameters, necessitating difficult judgment calls about tradeoffs, budgets, and search bounds. To address these issues and propose a practical method for robustly tuning large models, we present Cost-Aware Pareto Region Bayesian Search (CARBS), a Bayesian optimization algorithm that performs local search around the performance-cost Pareto frontier. CARBS does well even in unbounded search spaces with many hyperparameters, learns scaling relationships so that it can tune models even as they are scaled up, and automates much of the "black magic" of tuning. Among our results, we effectively solve the entire ProcGen benchmark just by tuning a simple baseline (PPO, as provided in the original ProcGen paper). We also reproduce the model size vs. training tokens scaling result from the Chinchilla project (Hoffmann et al. 2022), while simultaneously discovering scaling laws for every other hyperparameter, via an easy automated process that uses significantly less compute and is applicable to any deep learning problem (not just language models).

Avalon: A Benchmark for RL Generalization Using Procedurally Generated Worlds

Despite impressive successes, deep reinforcement learning (RL) systems still fall short of human performance on generalization to new tasks and environments that differ from their training. As a benchmark tailored for studying RL generalization, we introduce Avalon, a set of tasks in which embodied agents in highly diverse procedural 3D worlds must survive by navigating terrain, hunting or gathering food, and avoiding hazards. Avalon is unique among existing RL benchmarks in that the reward function, world dynamics, and action space are the same for every task, with tasks differentiated solely by altering the environment; its 20 tasks, ranging in complexity from eat and throw to hunt and navigate, each create worlds in which the agent must perform specific skills in order to survive. This setup enables investigations of generalization within tasks, between tasks, and to compositional tasks that require combining skills learned from previous tasks. Avalon includes a highly efficient simulator, a library of baselines, and a benchmark with scoring metrics evaluated against hundreds of hours of human performance, all of which are open-source and publicly available. We find that standard RL baselines make progress on most tasks but are still far from human performance, suggesting Avalon is challenging enough to advance the quest for generalizable RL.

FusedProp: Towards Efficient Training of Generative Adversarial Networks

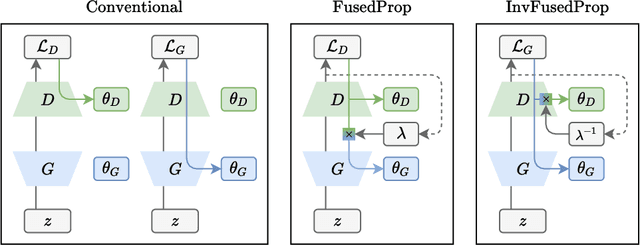
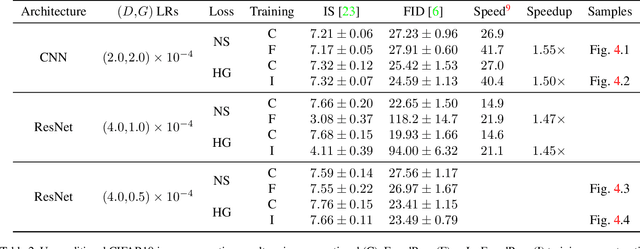
Generative adversarial networks (GANs) are capable of generating strikingly realistic samples but state-of-the-art GANs can be extremely computationally expensive to train. In this paper, we propose the fused propagation (FusedProp) algorithm which can be used to efficiently train the discriminator and the generator of common GANs simultaneously using only one forward and one backward propagation. We show that FusedProp achieves 1.49 times the training speed compared to the conventional training of GANs, although further studies are required to improve its stability. By reporting our preliminary results and open-sourcing our implementation, we hope to accelerate future research on the training of GANs.

A Networks and Machine Learning Approach to Determine the Best College Coaches of the 20th-21st Centuries

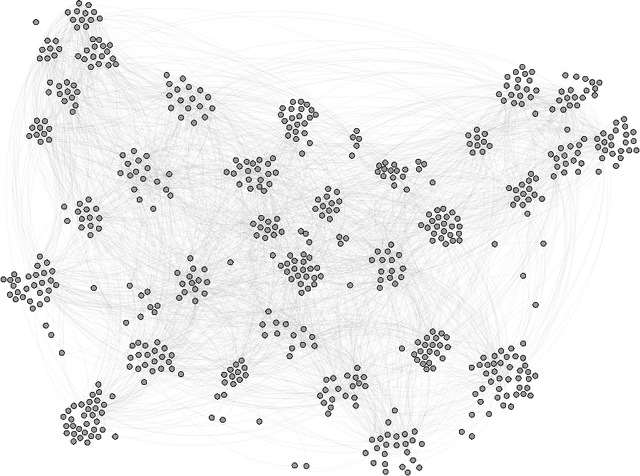
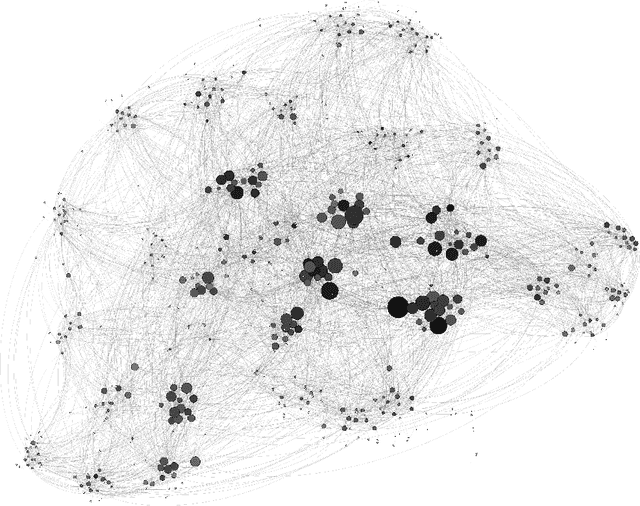
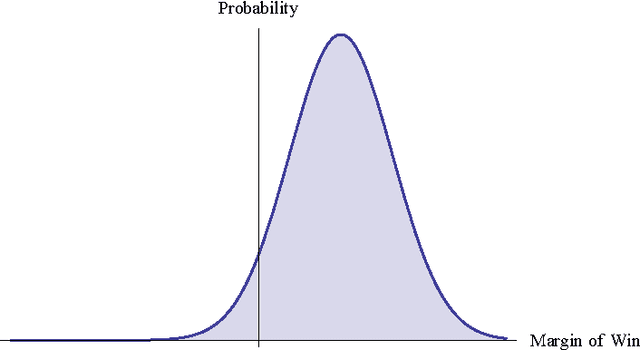
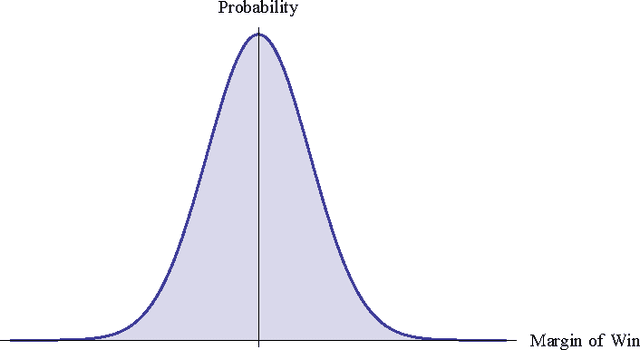
Our objective is to find the five best college sports coaches of past century for three different sports. We decided to look at men's basketball, football, and baseball. We wanted to use an approach that could definitively determine team skill from the games played, and then use a machine-learning algorithm to calculate the correct coach skills for each team in a given year. We created a networks-based model to calculate team skill from historical game data. A digraph was created for each year in each sport. Nodes represented teams, and edges represented a game played between two teams. The arrowhead pointed towards the losing team. We calculated the team skill of each graph using a right-hand eigenvector centrality measure. This way, teams that beat good teams will be ranked higher than teams that beat mediocre teams. The eigenvector centrality rankings for most years were well correlated with tournament performance and poll-based rankings. We assumed that the relationship between coach skill $C_s$, player skill $P_s$, and team skill $T_s$ was $C_s \cdot P_s = T_s$. We then created a function to describe the probability that a given score difference would occur based on player skill and coach skill. We multiplied the probabilities of all edges in the network together to find the probability that the correct network would occur with any given player skill and coach skill matrix. We was able to determine player skill as a function of team skill and coach skill, eliminating the need to optimize two unknown matrices. The top five coaches in each year were noted, and the top coach of all time was calculated by dividing the number of times that coach ranked in the yearly top five by the years said coach had been active.