Sharp asymptotics on the compression of two-layer neural networks

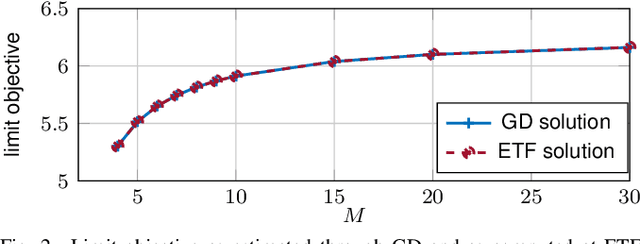
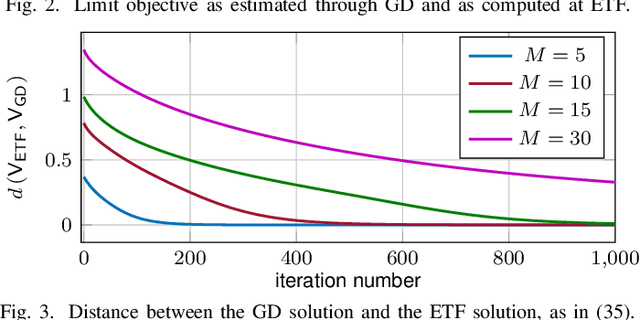
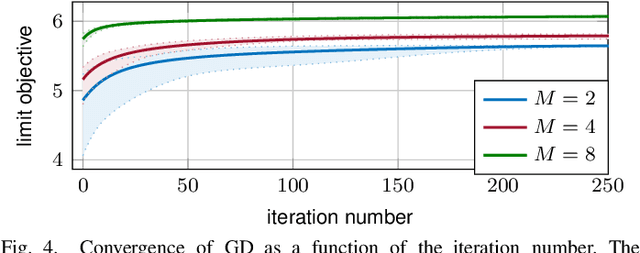
In this paper, we study the compression of a target two-layer neural network with N nodes into a compressed network with M < N nodes. More precisely, we consider the setting in which the weights of the target network are i.i.d. sub-Gaussian, and we minimize the population L2 loss between the outputs of the target and of the compressed network, under the assumption of Gaussian inputs. By using tools from high-dimensional probability, we show that this non-convex problem can be simplified when the target network is sufficiently over-parameterized, and provide the error rate of this approximation as a function of the input dimension and N . For a ReLU activation function, we conjecture that the optimum of the simplified optimization problem is achieved by taking weights on the Equiangular Tight Frame (ETF), while the scaling of the weights and the orientation of the ETF depend on the parameters of the target network. Numerical evidence is provided to support this conjecture.