Almost Tight Error Bounds on Differentially Private Continual Counting

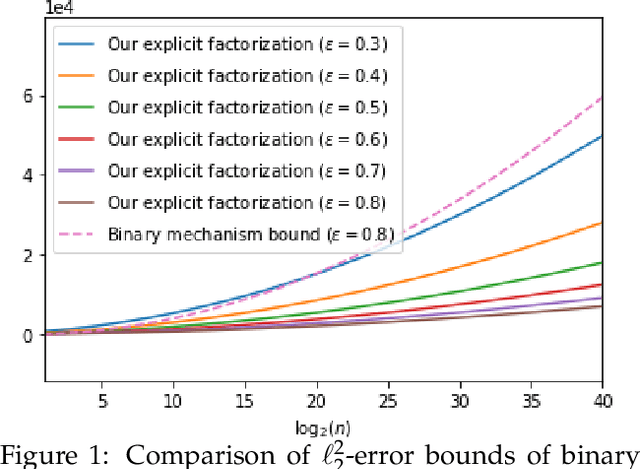
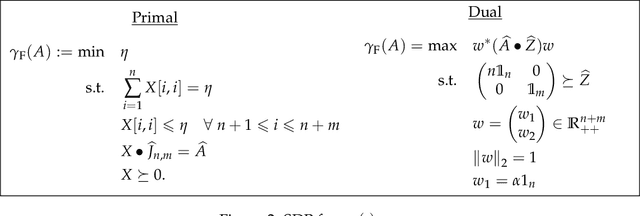
The first large-scale deployment of private federated learning uses differentially private counting in the continual release model as a subroutine (Google AI blog titled "Federated Learning with Formal Differential Privacy Guarantees"). In this case, a concrete bound on the error is very relevant to reduce the privacy parameter. The standard mechanism for continual counting is the binary mechanism. We present a novel mechanism and show that its mean squared error is both asymptotically optimal and a factor 10 smaller than the error of the binary mechanism. We also show that the constants in our analysis are almost tight by giving non-asymptotic lower and upper bounds that differ only in the constants of lower-order terms. Our algorithm is a matrix mechanism for the counting matrix and takes constant time per release. We also use our explicit factorization of the counting matrix to give an upper bound on the excess risk of the private learning algorithm of Denisov et al. (NeurIPS 2022). Our lower bound for any continual counting mechanism is the first tight lower bound on continual counting under approximate differential privacy. It is achieved using a new lower bound on a certain factorization norm, denoted by $\gamma_F(\cdot)$, in terms of the singular values of the matrix. In particular, we show that for any complex matrix, $A \in \mathbb{C}^{m \times n}$, \[ \gamma_F(A) \geq \frac{1}{\sqrt{m}}\|A\|_1, \] where $\|\cdot \|$ denotes the Schatten-1 norm. We believe this technique will be useful in proving lower bounds for a larger class of linear queries. To illustrate the power of this technique, we show the first lower bound on the mean squared error for answering parity queries.