A Unifying Framework for Differentially Private Sums under Continual Observation

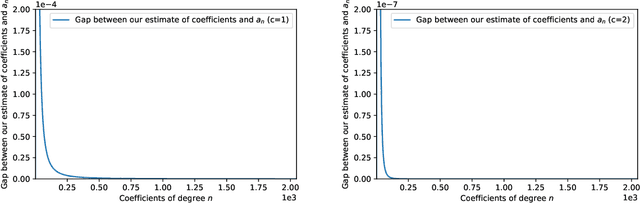
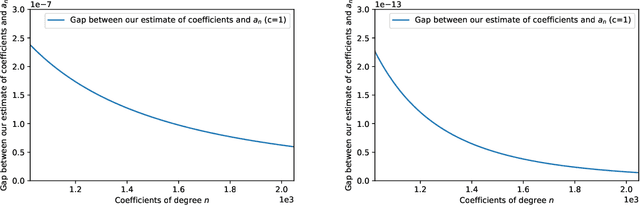
We study the problem of maintaining a differentially private decaying sum under continual observation. We give a unifying framework and an efficient algorithm for this problem for \emph{any sufficiently smooth} function. Our algorithm is the first differentially private algorithm that does not have a multiplicative error for polynomially-decaying weights. Our algorithm improves on all prior works on differentially private decaying sums under continual observation and recovers exactly the additive error for the special case of continual counting from Henzinger et al. (SODA 2023) as a corollary. Our algorithm is a variant of the factorization mechanism whose error depends on the $\gamma_2$ and $\gamma_F$ norm of the underlying matrix. We give a constructive proof for an almost exact upper bound on the $\gamma_2$ and $\gamma_F$ norm and an almost tight lower bound on the $\gamma_2$ norm for a large class of lower-triangular matrices. This is the first non-trivial lower bound for lower-triangular matrices whose non-zero entries are not all the same. It includes matrices for all continual decaying sums problems, resulting in an upper bound on the additive error of any differentially private decaying sums algorithm under continual observation. We also explore some implications of our result in discrepancy theory and operator algebra. Given the importance of the $\gamma_2$ norm in computer science and the extensive work in mathematics, we believe our result will have further applications.

Almost Tight Error Bounds on Differentially Private Continual Counting

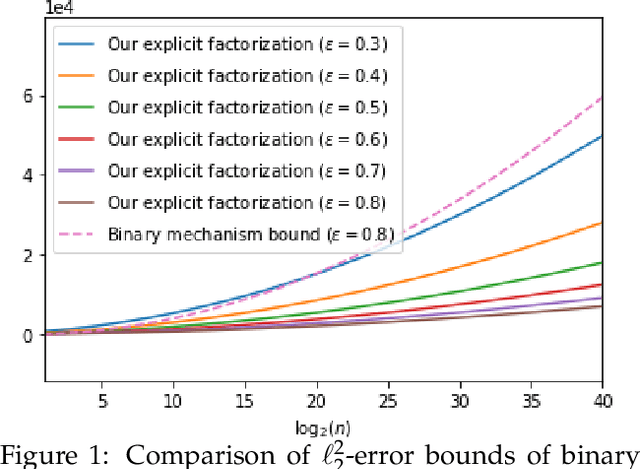
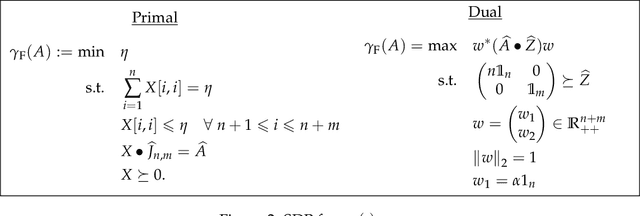
The first large-scale deployment of private federated learning uses differentially private counting in the continual release model as a subroutine (Google AI blog titled "Federated Learning with Formal Differential Privacy Guarantees"). In this case, a concrete bound on the error is very relevant to reduce the privacy parameter. The standard mechanism for continual counting is the binary mechanism. We present a novel mechanism and show that its mean squared error is both asymptotically optimal and a factor 10 smaller than the error of the binary mechanism. We also show that the constants in our analysis are almost tight by giving non-asymptotic lower and upper bounds that differ only in the constants of lower-order terms. Our algorithm is a matrix mechanism for the counting matrix and takes constant time per release. We also use our explicit factorization of the counting matrix to give an upper bound on the excess risk of the private learning algorithm of Denisov et al. (NeurIPS 2022). Our lower bound for any continual counting mechanism is the first tight lower bound on continual counting under approximate differential privacy. It is achieved using a new lower bound on a certain factorization norm, denoted by $\gamma_F(\cdot)$, in terms of the singular values of the matrix. In particular, we show that for any complex matrix, $A \in \mathbb{C}^{m \times n}$, \[ \gamma_F(A) \geq \frac{1}{\sqrt{m}}\|A\|_1, \] where $\|\cdot \|$ denotes the Schatten-1 norm. We believe this technique will be useful in proving lower bounds for a larger class of linear queries. To illustrate the power of this technique, we show the first lower bound on the mean squared error for answering parity queries.

A Framework for Private Matrix Analysis

We study private matrix analysis in the sliding window model where only the last $W$ updates to matrices are considered useful for analysis. We give first efficient $o(W)$ space differentially private algorithms for spectral approximation, principal component analysis, and linear regression. We also initiate and show efficient differentially private algorithms for two important variants of principal component analysis: sparse principal component analysis and non-negative principal component analysis. Prior to our work, no such result was known for sparse and non-negative differentially private principal component analysis even in the static data setting. These algorithms are obtained by identifying sufficient conditions on positive semidefinite matrices formed from streamed matrices. We also show a lower bound on space required to compute low-rank approximation even if the algorithm gives multiplicative approximation and incurs additive error. This follows via reduction to a certain communication complexity problem.