Nimbus: A Unified Embodied Synthetic Data Generation Framework

Scaling data volume and diversity is critical for generalizing embodied intelligence. While synthetic data generation offers a scalable alternative to expensive physical data acquisition, existing pipelines remain fragmented and task-specific. This isolation leads to significant engineering inefficiency and system instability, failing to support the sustained, high-throughput data generation required for foundation model training. To address these challenges, we present Nimbus, a unified synthetic data generation framework designed to integrate heterogeneous navigation and manipulation pipelines. Nimbus introduces a modular four-layer architecture featuring a decoupled execution model that separates trajectory planning, rendering, and storage into asynchronous stages. By implementing dynamic pipeline scheduling, global load balancing, distributed fault tolerance, and backend-specific rendering optimizations, the system maximizes resource utilization across CPU, GPU, and I/O resources. Our evaluation demonstrates that Nimbus achieves a 2-3X improvement in end-to-end throughput compared to unoptimized baselines and ensuring robust, long-term operation in large-scale distributed environments. This framework serves as the production backbone for the InternData suite, enabling seamless cross-domain data synthesis.

InternVLA-A1: Unifying Understanding, Generation and Action for Robotic Manipulation

Prevalent Vision-Language-Action (VLA) models are typically built upon Multimodal Large Language Models (MLLMs) and demonstrate exceptional proficiency in semantic understanding, but they inherently lack the capability to deduce physical world dynamics. Consequently, recent approaches have shifted toward World Models, typically formulated via video prediction; however, these methods often suffer from a lack of semantic grounding and exhibit brittleness when handling prediction errors. To synergize semantic understanding with dynamic predictive capabilities, we present InternVLA-A1. This model employs a unified Mixture-of-Transformers architecture, coordinating three experts for scene understanding, visual foresight generation, and action execution. These components interact seamlessly through a unified masked self-attention mechanism. Building upon InternVL3 and Qwen3-VL, we instantiate InternVLA-A1 at 2B and 3B parameter scales. We pre-train these models on hybrid synthetic-real datasets spanning InternData-A1 and Agibot-World, covering over 533M frames. This hybrid training strategy effectively harnesses the diversity of synthetic simulation data while minimizing the sim-to-real gap. We evaluated InternVLA-A1 across 12 real-world robotic tasks and simulation benchmark. It significantly outperforms leading models like pi0 and GR00T N1.5, achieving a 14.5\% improvement in daily tasks and a 40\%-73.3\% boost in dynamic settings, such as conveyor belt sorting.

Improving the accuracy and generalizability of molecular property regression models with a substructure-substitution-rule-informed framework

Artificial Intelligence (AI)-aided drug discovery is an active research field, yet AI models often exhibit poor accuracy in regression tasks for molecular property prediction, and perform catastrophically poorly for out-of-distribution (OOD) molecules. Here, we present MolRuleLoss, a substructure-substitution-rule-informed framework that improves the accuracy and generalizability of multiple molecular property regression models (MPRMs) such as GEM and UniMol for diverse molecular property prediction tasks. MolRuleLoss incorporates partial derivative constraints for substructure substitution rules (SSRs) into an MPRM's loss function. When using GEM models for predicting lipophilicity, water solubility, and solvation-free energy (using lipophilicity, ESOL, and freeSolv datasets from MoleculeNet), the root mean squared error (RMSE) values with and without MolRuleLoss were 0.587 vs. 0.660, 0.777 vs. 0.798, and 1.252 vs. 1.877, respectively, representing 2.6-33.3% performance improvements. We show that both the number and the quality of SSRs contribute to the magnitude of prediction accuracy gains obtained upon adding MolRuleLoss to an MPRM. MolRuleLoss improved the generalizability of MPRMs for "activity cliff" molecules in a lipophilicity prediction task and improved the generalizability of MPRMs for OOD molecules in a melting point prediction task. In a molecular weight prediction task for OOD molecules, MolRuleLoss reduced the RMSE value of a GEM model from 29.507 to 0.007. We also provide a formal demonstration that the upper bound of the variation for property change of SSRs is positively correlated with an MPRM's error. Together, we show that using the MolRuleLoss framework as a bolt-on boosts the prediction accuracy and generalizability of multiple MPRMs, supporting diverse applications in areas like cheminformatics and AI-aided drug discovery.

Open Multimodal Retrieval-Augmented Factual Image Generation

Large Multimodal Models (LMMs) have achieved remarkable progress in generating photorealistic and prompt-aligned images, but they often produce outputs that contradict verifiable knowledge, especially when prompts involve fine-grained attributes or time-sensitive events. Conventional retrieval-augmented approaches attempt to address this issue by introducing external information, yet they are fundamentally incapable of grounding generation in accurate and evolving knowledge due to their reliance on static sources and shallow evidence integration. To bridge this gap, we introduce ORIG, an agentic open multimodal retrieval-augmented framework for Factual Image Generation (FIG), a new task that requires both visual realism and factual grounding. ORIG iteratively retrieves and filters multimodal evidence from the web and incrementally integrates the refined knowledge into enriched prompts to guide generation. To support systematic evaluation, we build FIG-Eval, a benchmark spanning ten categories across perceptual, compositional, and temporal dimensions. Experiments demonstrate that ORIG substantially improves factual consistency and overall image quality over strong baselines, highlighting the potential of open multimodal retrieval for factual image generation.

InstructVLA: Vision-Language-Action Instruction Tuning from Understanding to Manipulation

To operate effectively in the real world, robots must integrate multimodal reasoning with precise action generation. However, existing vision-language-action (VLA) models often sacrifice one for the other, narrow their abilities to task-specific manipulation data, and suffer catastrophic forgetting of pre-trained vision-language capabilities. To bridge this gap, we introduce InstructVLA, an end-to-end VLA model that preserves the flexible reasoning of large vision-language models (VLMs) while delivering leading manipulation performance. InstructVLA introduces a novel training paradigm, Vision-Language-Action Instruction Tuning (VLA-IT), which employs multimodal training with mixture-of-experts adaptation to jointly optimize textual reasoning and action generation on both standard VLM corpora and a curated 650K-sample VLA-IT dataset. On in-domain SimplerEnv tasks, InstructVLA achieves 30.5% improvement over SpatialVLA. To evaluate generalization, we introduce SimplerEnv-Instruct, an 80-task benchmark requiring closed-loop control and high-level instruction understanding, where it outperforms a fine-tuned OpenVLA by 92% and an action expert aided by GPT-4o by 29%. Additionally, InstructVLA surpasses baseline VLMs on multimodal tasks and exhibits inference-time scaling by leveraging textual reasoning to boost manipulation performance in both simulated and real-world settings. These results demonstrate InstructVLA's potential for bridging intuitive and steerable human-robot interaction with efficient policy learning.

The Medium Is Not the Message: Deconfounding Text Embeddings via Linear Concept Erasure

Embedding-based similarity metrics between text sequences can be influenced not just by the content dimensions we most care about, but can also be biased by spurious attributes like the text's source or language. These document confounders cause problems for many applications, but especially those that need to pool texts from different corpora. This paper shows that a debiasing algorithm that removes information about observed confounders from the encoder representations substantially reduces these biases at a minimal computational cost. Document similarity and clustering metrics improve across every embedding variant and task we evaluate -- often dramatically. Interestingly, performance on out-of-distribution benchmarks is not impacted, indicating that the embeddings are not otherwise degraded.

CronusVLA: Transferring Latent Motion Across Time for Multi-Frame Prediction in Manipulation

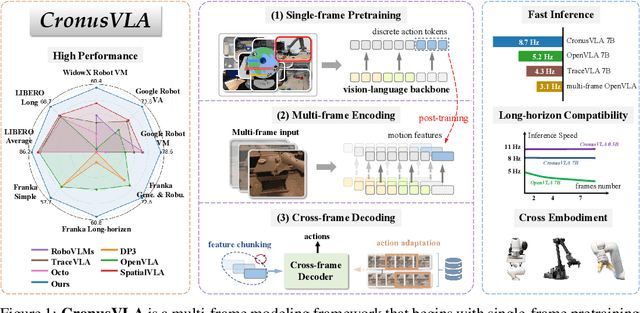
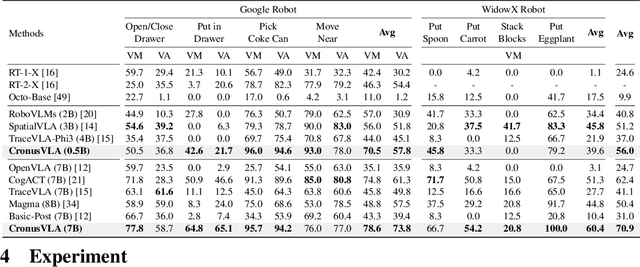
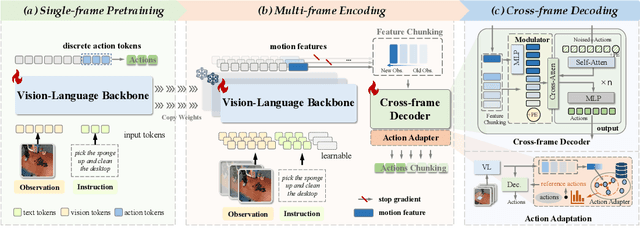
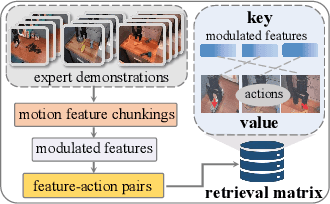
Recent vision-language-action (VLA) models built on pretrained vision-language models (VLMs) have demonstrated strong generalization across manipulation tasks. However, they remain constrained by a single-frame observation paradigm and cannot fully benefit from the motion information offered by aggregated multi-frame historical observations, as the large vision-language backbone introduces substantial computational cost and inference latency. We propose CronusVLA, a unified framework that extends single-frame VLA models to the multi-frame paradigm through an efficient post-training stage. CronusVLA comprises three key components: (1) single-frame pretraining on large-scale embodied datasets with autoregressive action tokens prediction, which establishes an embodied vision-language foundation; (2) multi-frame encoding, adapting the prediction of vision-language backbones from discrete action tokens to motion features during post-training, and aggregating motion features from historical frames into a feature chunking; (3) cross-frame decoding, which maps the feature chunking to accurate actions via a shared decoder with cross-attention. By reducing redundant token computation and caching past motion features, CronusVLA achieves efficient inference. As an application of motion features, we further propose an action adaptation mechanism based on feature-action retrieval to improve model performance during finetuning. CronusVLA achieves state-of-the-art performance on SimplerEnv with 70.9% success rate, and 12.7% improvement over OpenVLA on LIBERO. Real-world Franka experiments also show the strong performance and robustness.

GENMANIP: LLM-driven Simulation for Generalizable Instruction-Following Manipulation

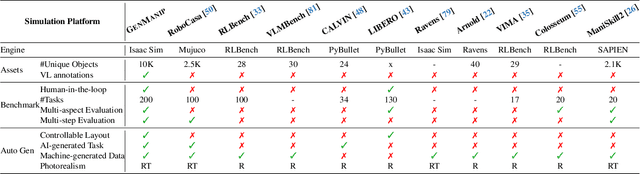
Robotic manipulation in real-world settings remains challenging, especially regarding robust generalization. Existing simulation platforms lack sufficient support for exploring how policies adapt to varied instructions and scenarios. Thus, they lag behind the growing interest in instruction-following foundation models like LLMs, whose adaptability is crucial yet remains underexplored in fair comparisons. To bridge this gap, we introduce GenManip, a realistic tabletop simulation platform tailored for policy generalization studies. It features an automatic pipeline via LLM-driven task-oriented scene graph to synthesize large-scale, diverse tasks using 10K annotated 3D object assets. To systematically assess generalization, we present GenManip-Bench, a benchmark of 200 scenarios refined via human-in-the-loop corrections. We evaluate two policy types: (1) modular manipulation systems integrating foundation models for perception, reasoning, and planning, and (2) end-to-end policies trained through scalable data collection. Results show that while data scaling benefits end-to-end methods, modular systems enhanced with foundation models generalize more effectively across diverse scenarios. We anticipate this platform to facilitate critical insights for advancing policy generalization in realistic conditions. Project Page: https://genmanip.axi404.top/.

LEXam: Benchmarking Legal Reasoning on 340 Law Exams

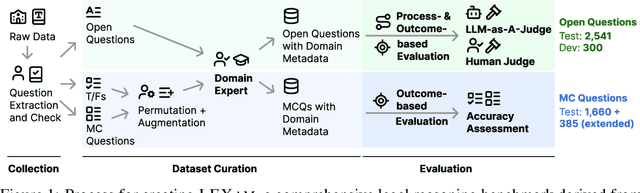
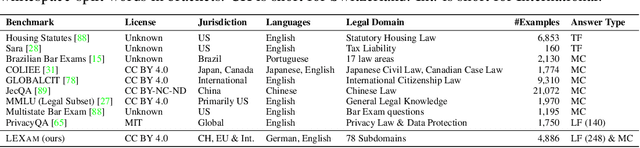
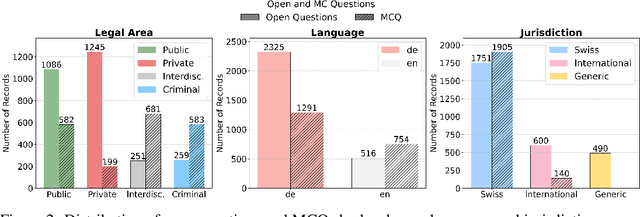
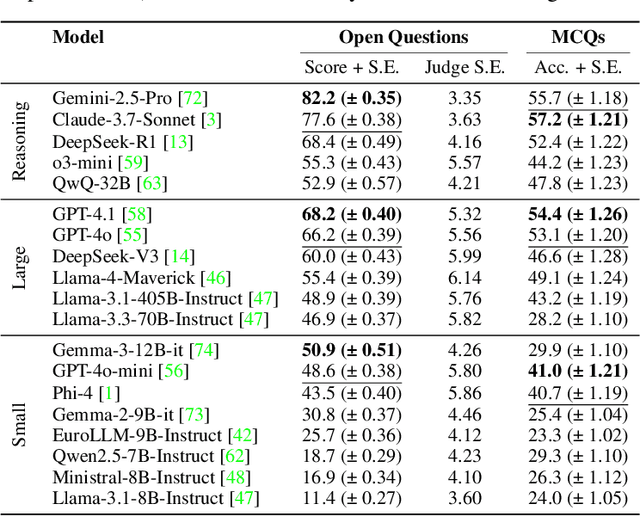
Long-form legal reasoning remains a key challenge for large language models (LLMs) in spite of recent advances in test-time scaling. We introduce LEXam, a novel benchmark derived from 340 law exams spanning 116 law school courses across a range of subjects and degree levels. The dataset comprises 4,886 law exam questions in English and German, including 2,841 long-form, open-ended questions and 2,045 multiple-choice questions. Besides reference answers, the open questions are also accompanied by explicit guidance outlining the expected legal reasoning approach such as issue spotting, rule recall, or rule application. Our evaluation on both open-ended and multiple-choice questions present significant challenges for current LLMs; in particular, they notably struggle with open questions that require structured, multi-step legal reasoning. Moreover, our results underscore the effectiveness of the dataset in differentiating between models with varying capabilities. Adopting an LLM-as-a-Judge paradigm with rigorous human expert validation, we demonstrate how model-generated reasoning steps can be evaluated consistently and accurately. Our evaluation setup provides a scalable method to assess legal reasoning quality beyond simple accuracy metrics. Project page: https://lexam-benchmark.github.io/

Gripper Keypose and Object Pointflow as Interfaces for Bimanual Robotic Manipulation

Bimanual manipulation is a challenging yet crucial robotic capability, demanding precise spatial localization and versatile motion trajectories, which pose significant challenges to existing approaches. Existing approaches fall into two categories: keyframe-based strategies, which predict gripper poses in keyframes and execute them via motion planners, and continuous control methods, which estimate actions sequentially at each timestep. The keyframe-based method lacks inter-frame supervision, struggling to perform consistently or execute curved motions, while the continuous method suffers from weaker spatial perception. To address these issues, this paper introduces an end-to-end framework PPI (keyPose and Pointflow Interface), which integrates the prediction of target gripper poses and object pointflow with the continuous actions estimation. These interfaces enable the model to effectively attend to the target manipulation area, while the overall framework guides diverse and collision-free trajectories. By combining interface predictions with continuous actions estimation, PPI demonstrates superior performance in diverse bimanual manipulation tasks, providing enhanced spatial localization and satisfying flexibility in handling movement restrictions. In extensive evaluations, PPI significantly outperforms prior methods in both simulated and real-world experiments, achieving state-of-the-art performance with a +16.1% improvement on the RLBench2 simulation benchmark and an average of +27.5% gain across four challenging real-world tasks. Notably, PPI exhibits strong stability, high precision, and remarkable generalization capabilities in real-world scenarios. Project page: https://yuyinyang3y.github.io/PPI/