Exploiting Edge Features for Transferable Adversarial Attacks in Distributed Machine Learning

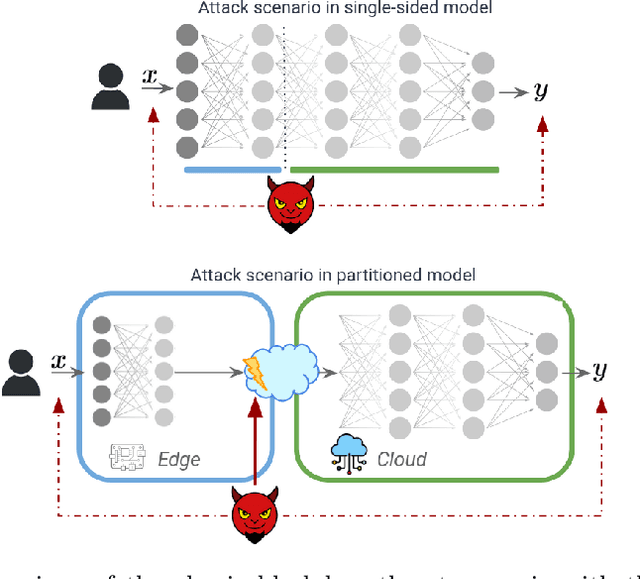
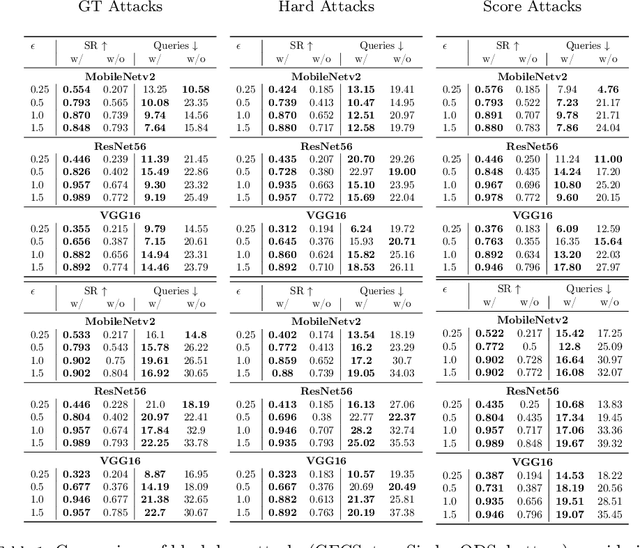
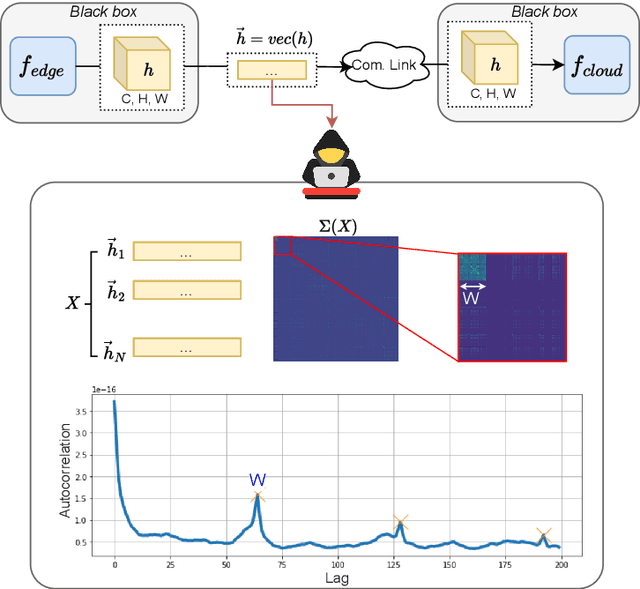
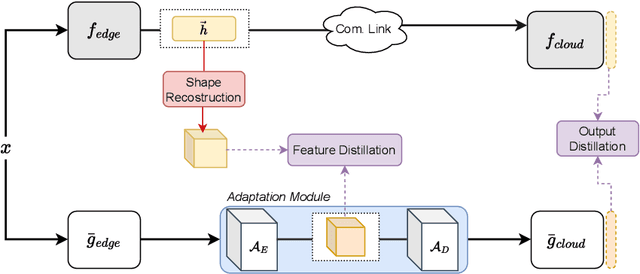
As machine learning models become increasingly deployed across the edge of internet of things environments, a partitioned deep learning paradigm in which models are split across multiple computational nodes introduces a new dimension of security risk. Unlike traditional inference setups, these distributed pipelines span the model computation across heterogeneous nodes and communication layers, thereby exposing a broader attack surface to potential adversaries. Building on these motivations, this work explores a previously overlooked vulnerability: even when both the edge and cloud components of the model are inaccessible (i.e., black-box), an adversary who intercepts the intermediate features transmitted between them can still pose a serious threat. We demonstrate that, under these mild and realistic assumptions, an attacker can craft highly transferable proxy models, making the entire deep learning system significantly more vulnerable to evasion attacks. In particular, the intercepted features can be effectively analyzed and leveraged to distill surrogate models capable of crafting highly transferable adversarial examples against the target model. To this end, we propose an exploitation strategy specifically designed for distributed settings, which involves reconstructing the original tensor shape from vectorized transmitted features using simple statistical analysis, and adapting surrogate architectures accordingly to enable effective feature distillation. A comprehensive and systematic experimental evaluation has been conducted to demonstrate that surrogate models trained with the proposed strategy, i.e., leveraging intermediate features, tremendously improve the transferability of adversarial attacks. These findings underscore the urgent need to account for intermediate feature leakage in the design of secure distributed deep learning systems.

Video Deblurring by Sharpness Prior Detection and Edge Information

Video deblurring is essential task for autonomous driving, facial recognition, and security surveillance. Traditional methods directly estimate motion blur kernels, often introducing artifacts and leading to poor results. Recent approaches utilize the detection of sharp frames within video sequences to enhance deblurring. However, existing datasets rely on fixed number of sharp frames, which may be too restrictive for some applications and may introduce a bias during model training. To address these limitations and enhance domain adaptability, this work first introduces GoPro Random Sharp (GoProRS), a new dataset where the the frequency of sharp frames within the sequence is customizable, allowing more diverse training and testing scenarios. Furthermore, it presents a novel video deblurring model, called SPEINet, that integrates sharp frame features into blurry frame reconstruction through an attention-based encoder-decoder architecture, a lightweight yet robust sharp frame detection and an edge extraction phase. Extensive experimental results demonstrate that SPEINet outperforms state-of-the-art methods across multiple datasets, achieving an average of +3.2% PSNR improvement over recent techniques. Given such promising results, we believe that both the proposed model and dataset pave the way for future advancements in video deblurring based on the detection of sharp frames.

1-Lipschitz Layers Compared: Memory, Speed, and Certifiable Robustness

The robustness of neural networks against input perturbations with bounded magnitude represents a serious concern in the deployment of deep learning models in safety-critical systems. Recently, the scientific community has focused on enhancing certifiable robustness guarantees by crafting 1-Lipschitz neural networks that leverage Lipschitz bounded dense and convolutional layers. Although different methods have been proposed in the literature to achieve this goal, understanding the performance of such methods is not straightforward, since different metrics can be relevant (e.g., training time, memory usage, accuracy, certifiable robustness) for different applications. For this reason, this work provides a thorough theoretical and empirical comparison between methods by evaluating them in terms of memory usage, speed, and certifiable robust accuracy. The paper also provides some guidelines and recommendations to support the user in selecting the methods that work best depending on the available resources. We provide code at https://github.com/berndprach/1LipschitzLayersCompared.

Robust-by-Design Classification via Unitary-Gradient Neural Networks

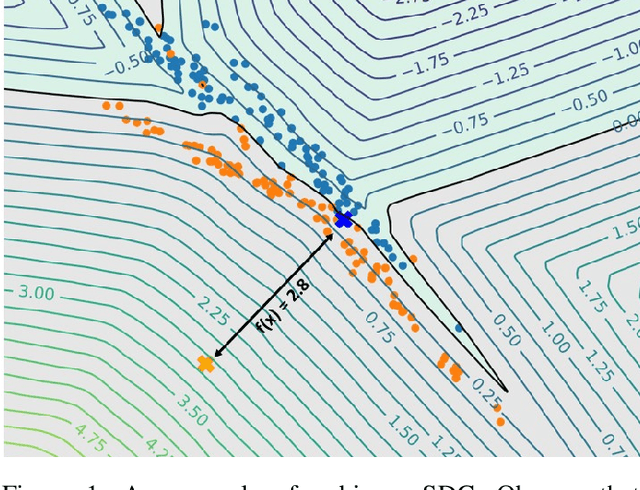
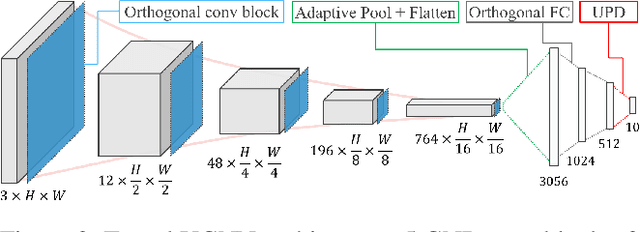
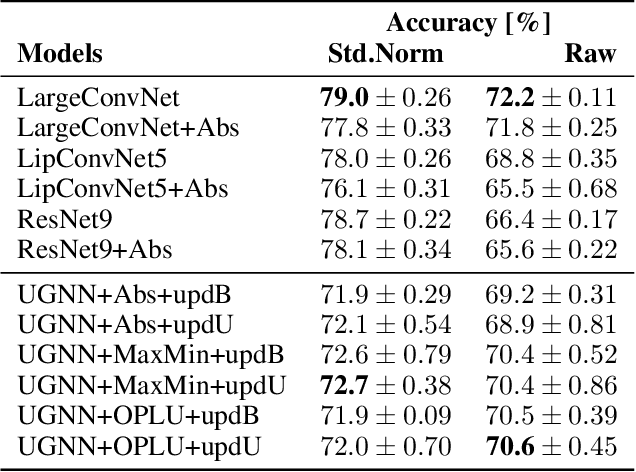
The use of neural networks in safety-critical systems requires safe and robust models, due to the existence of adversarial attacks. Knowing the minimal adversarial perturbation of any input x, or, equivalently, knowing the distance of x from the classification boundary, allows evaluating the classification robustness, providing certifiable predictions. Unfortunately, state-of-the-art techniques for computing such a distance are computationally expensive and hence not suited for online applications. This work proposes a novel family of classifiers, namely Signed Distance Classifiers (SDCs), that, from a theoretical perspective, directly output the exact distance of x from the classification boundary, rather than a probability score (e.g., SoftMax). SDCs represent a family of robust-by-design classifiers. To practically address the theoretical requirements of a SDC, a novel network architecture named Unitary-Gradient Neural Network is presented. Experimental results show that the proposed architecture approximates a signed distance classifier, hence allowing an online certifiable classification of x at the cost of a single inference.

Defending From Physically-Realizable Adversarial Attacks Through Internal Over-Activation Analysis

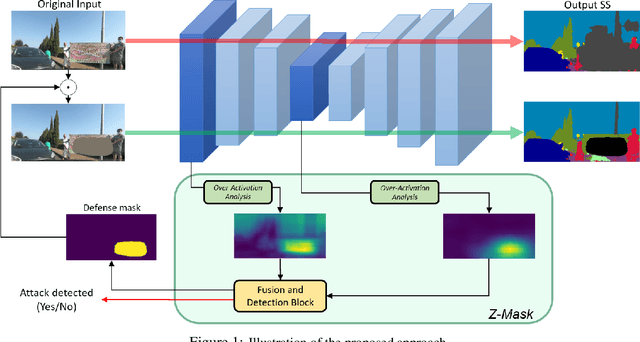
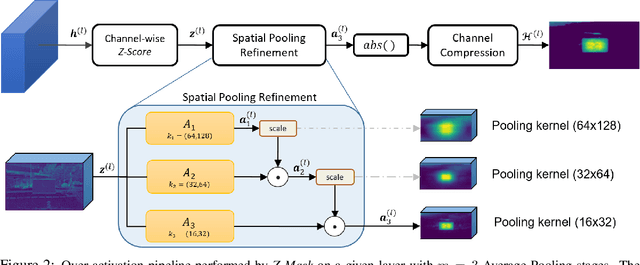
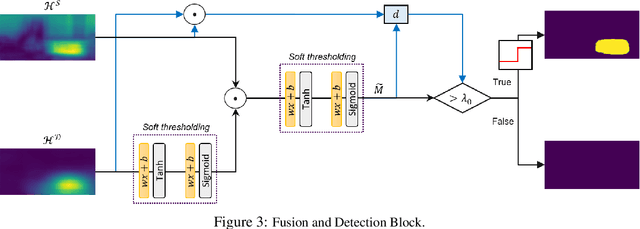
This work presents Z-Mask, a robust and effective strategy to improve the adversarial robustness of convolutional networks against physically-realizable adversarial attacks. The presented defense relies on specific Z-score analysis performed on the internal network features to detect and mask the pixels corresponding to adversarial objects in the input image. To this end, spatially contiguous activations are examined in shallow and deep layers to suggest potential adversarial regions. Such proposals are then aggregated through a multi-thresholding mechanism. The effectiveness of Z-Mask is evaluated with an extensive set of experiments carried out on models for both semantic segmentation and object detection. The evaluation is performed with both digital patches added to the input images and printed patches positioned in the real world. The obtained results confirm that Z-Mask outperforms the state-of-the-art methods in terms of both detection accuracy and overall performance of the networks under attack. Additional experiments showed that Z-Mask is also robust against possible defense-aware attacks.

On the Minimal Adversarial Perturbation for Deep Neural Networks with Provable Estimation Error

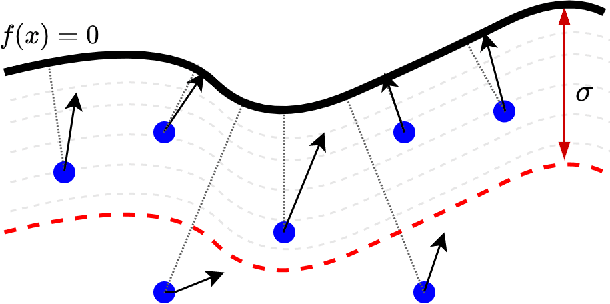
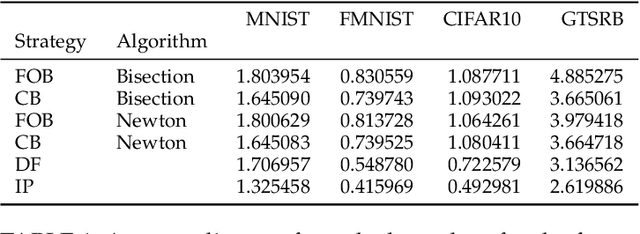
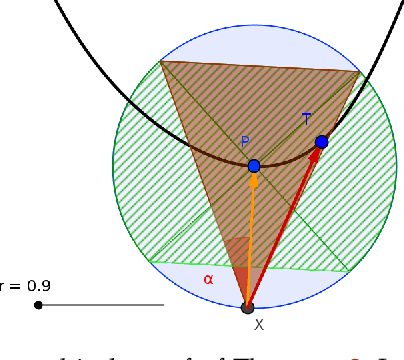
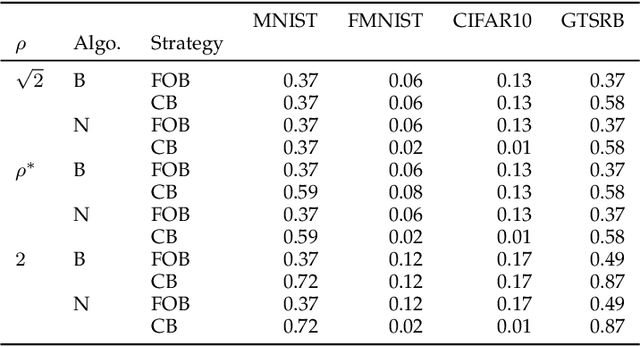
Although Deep Neural Networks (DNNs) have shown incredible performance in perceptive and control tasks, several trustworthy issues are still open. One of the most discussed topics is the existence of adversarial perturbations, which has opened an interesting research line on provable techniques capable of quantifying the robustness of a given input. In this regard, the Euclidean distance of the input from the classification boundary denotes a well-proved robustness assessment as the minimal affordable adversarial perturbation. Unfortunately, computing such a distance is highly complex due the non-convex nature of NNs. Despite several methods have been proposed to address this issue, to the best of our knowledge, no provable results have been presented to estimate and bound the error committed. This paper addresses this issue by proposing two lightweight strategies to find the minimal adversarial perturbation. Differently from the state-of-the-art, the proposed approach allows formulating an error estimation theory of the approximate distance with respect to the theoretical one. Finally, a substantial set of experiments is reported to evaluate the performance of the algorithms and support the theoretical findings. The obtained results show that the proposed strategies approximate the theoretical distance for samples close to the classification boundary, leading to provable robustness guarantees against any adversarial attacks.