Intriguing Properties of Robust Classification

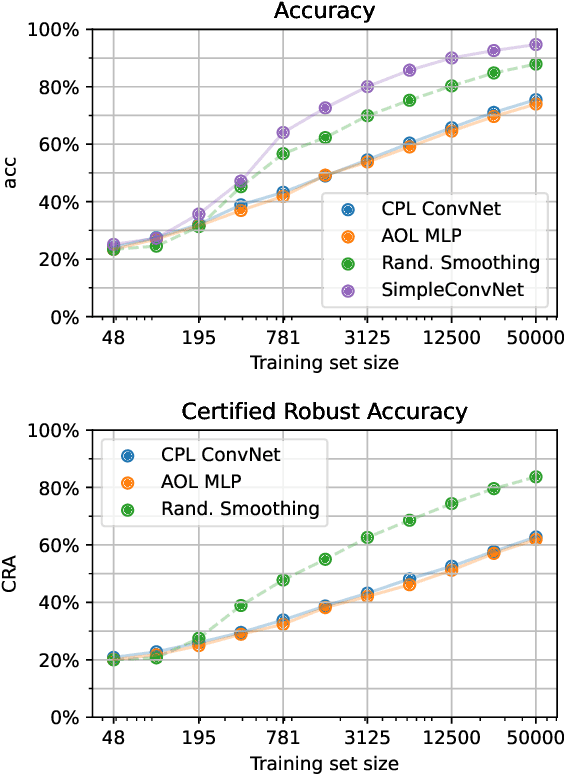
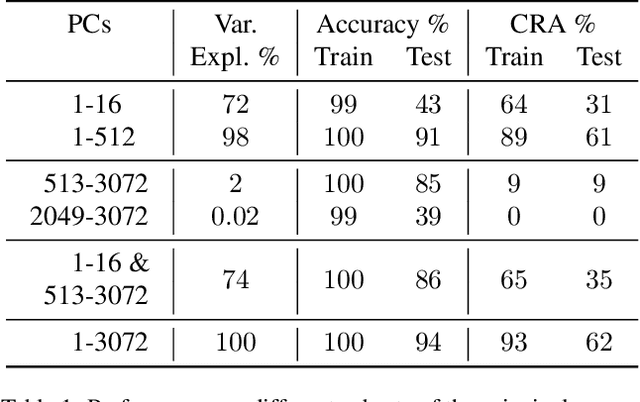
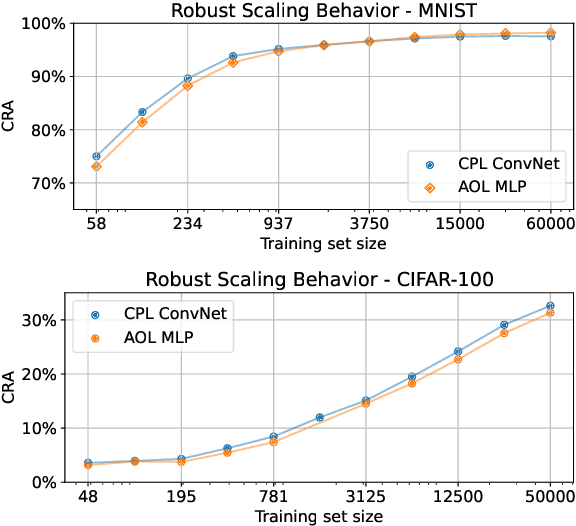
Despite extensive research since the community learned about adversarial examples 10 years ago, we still do not know how to train high-accuracy classifiers that are guaranteed to be robust to small perturbations of their inputs. Previous works often argued that this might be because no classifier exists that is robust and accurate at the same time. However, in computer vision this assumption does not match reality where humans are usually accurate and robust on most tasks of interest. We offer an alternative explanation and show that in certain settings robust generalization is only possible with unrealistically large amounts of data. More precisely we find a setting where a robust classifier exists, it is easy to learn an accurate classifier, yet it requires an exponential amount of data to learn a robust classifier. Based on this theoretical result, we explore how well robust classifiers generalize on datasets such as CIFAR-10. We come to the conclusion that on this datasets, the limitation of current robust models also lies in the generalization, and that they require a lot of data to do well on the test set. We also show that the problem is not in the expressiveness or generalization capabilities of current architectures, and that there are low magnitude features in the data which are useful for non-robust generalization but are not available for robust classifiers.

1-Lipschitz Layers Compared: Memory, Speed, and Certifiable Robustness

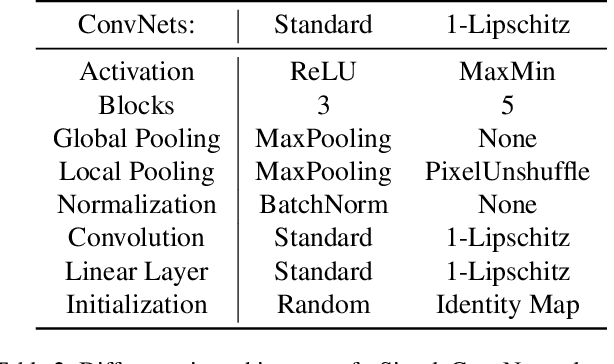
The robustness of neural networks against input perturbations with bounded magnitude represents a serious concern in the deployment of deep learning models in safety-critical systems. Recently, the scientific community has focused on enhancing certifiable robustness guarantees by crafting 1-Lipschitz neural networks that leverage Lipschitz bounded dense and convolutional layers. Although different methods have been proposed in the literature to achieve this goal, understanding the performance of such methods is not straightforward, since different metrics can be relevant (e.g., training time, memory usage, accuracy, certifiable robustness) for different applications. For this reason, this work provides a thorough theoretical and empirical comparison between methods by evaluating them in terms of memory usage, speed, and certifiable robust accuracy. The paper also provides some guidelines and recommendations to support the user in selecting the methods that work best depending on the available resources. We provide code at https://github.com/berndprach/1LipschitzLayersCompared.

1-Lipschitz Neural Networks are more expressive with N-Activations

A crucial property for achieving secure, trustworthy and interpretable deep learning systems is their robustness: small changes to a system's inputs should not result in large changes to its outputs. Mathematically, this means one strives for networks with a small Lipschitz constant. Several recent works have focused on how to construct such Lipschitz networks, typically by imposing constraints on the weight matrices. In this work, we study an orthogonal aspect, namely the role of the activation function. We show that commonly used activation functions, such as MaxMin, as well as all piece-wise linear ones with two segments unnecessarily restrict the class of representable functions, even in the simplest one-dimensional setting. We furthermore introduce the new N-activation function that is provably more expressive than currently popular activation functions. We provide code at https://github.com/berndprach/NActivation.

Almost-Orthogonal Layers for Efficient General-Purpose Lipschitz Networks

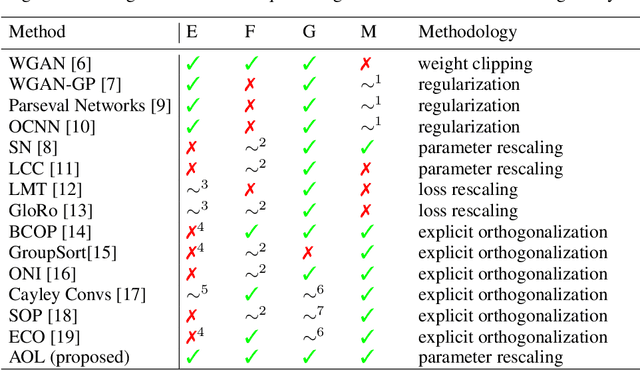
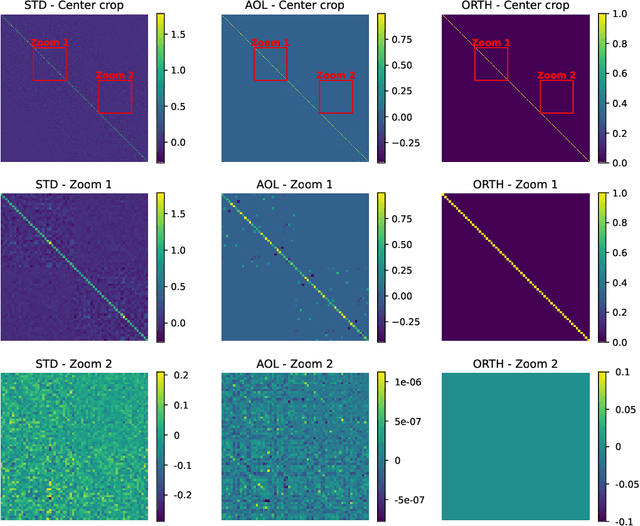
It is a highly desirable property for deep networks to be robust against small input changes. One popular way to achieve this property is by designing networks with a small Lipschitz constant. In this work, we propose a new technique for constructing such Lipschitz networks that has a number of desirable properties: it can be applied to any linear network layer (fully-connected or convolutional), it provides formal guarantees on the Lipschitz constant, it is easy to implement and efficient to run, and it can be combined with any training objective and optimization method. In fact, our technique is the first one in the literature that achieves all of these properties simultaneously. Our main contribution is a rescaling-based weight matrix parametrization that guarantees each network layer to have a Lipschitz constant of at most 1 and results in the learned weight matrices to be close to orthogonal. Hence we call such layers almost-orthogonal Lipschitz (AOL). Experiments and ablation studies in the context of image classification with certified robust accuracy confirm that AOL layers achieve results that are on par with most existing methods. Yet, they are simpler to implement and more broadly applicable, because they do not require computationally expensive matrix orthogonalization or inversion steps as part of the network architecture. We provide code at https://github.com/berndprach/AOL.