Recurrent Temporal Revision Graph Networks

Temporal graphs offer more accurate modeling of many real-world scenarios than static graphs. However, neighbor aggregation, a critical building block of graph networks, for temporal graphs, is currently straightforwardly extended from that of static graphs. It can be computationally expensive when involving all historical neighbors during such aggregation. In practice, typically only a subset of the most recent neighbors are involved. However, such subsampling leads to incomplete and biased neighbor information. To address this limitation, we propose a novel framework for temporal neighbor aggregation that uses the recurrent neural network with node-wise hidden states to integrate information from all historical neighbors for each node to acquire the complete neighbor information. We demonstrate the superior theoretical expressiveness of the proposed framework as well as its state-of-the-art performance in real-world applications. Notably, it achieves a significant +9.6% improvement on averaged precision in a real-world Ecommerce dataset over existing methods on 2-layer models.

Learning to Branch in Combinatorial Optimization with Graph Pointer Networks

Branch-and-bound is a typical way to solve combinatorial optimization problems. This paper proposes a graph pointer network model for learning the variable selection policy in the branch-and-bound. We extract the graph features, global features and historical features to represent the solver state. The proposed model, which combines the graph neural network and the pointer mechanism, can effectively map from the solver state to the branching variable decisions. The model is trained to imitate the classic strong branching expert rule by a designed top-k Kullback-Leibler divergence loss function. Experiments on a series of benchmark problems demonstrate that the proposed approach significantly outperforms the widely used expert-designed branching rules. Our approach also outperforms the state-of-the-art machine-learning-based branch-and-bound methods in terms of solving speed and search tree size on all the test instances. In addition, the model can generalize to unseen instances and scale to larger instances.

Clustered Embedding Learning for Recommender Systems

In recent years, recommender systems have advanced rapidly, where embedding learning for users and items plays a critical role. A standard method learns a unique embedding vector for each user and item. However, such a method has two important limitations in real-world applications: 1) it is hard to learn embeddings that generalize well for users and items with rare interactions on their own; and 2) it may incur unbearably high memory costs when the number of users and items scales up. Existing approaches either can only address one of the limitations or have flawed overall performances. In this paper, we propose Clustered Embedding Learning (CEL) as an integrated solution to these two problems. CEL is a plug-and-play embedding learning framework that can be combined with any differentiable feature interaction model. It is capable of achieving improved performance, especially for cold users and items, with reduced memory cost. CEL enables automatic and dynamic clustering of users and items in a top-down fashion, where clustered entities jointly learn a shared embedding. The accelerated version of CEL has an optimal time complexity, which supports efficient online updates. Theoretically, we prove the identifiability and the existence of a unique optimal number of clusters for CEL in the context of nonnegative matrix factorization. Empirically, we validate the effectiveness of CEL on three public datasets and one business dataset, showing its consistently superior performance against current state-of-the-art methods. In particular, when incorporating CEL into the business model, it brings an improvement of $+0.6\%$ in AUC, which translates into a significant revenue gain; meanwhile, the size of the embedding table gets $2650$ times smaller.

Towards Generalized Implementation of Wasserstein Distance in GANs

Wasserstein GANs (WGANs), built upon the Kantorovich-Rubinstein (KR) duality of Wasserstein distance, is one of the most theoretically sound GAN models. However, in practice it does not always outperform other variants of GANs. This is mostly due to the imperfect implementation of the Lipschitz condition required by the KR duality. Extensive work has been done in the community with different implementations of the Lipschitz constraint, which, however, is still hard to satisfy the restriction perfectly in practice. In this paper, we argue that the strong Lipschitz constraint might be unnecessary for optimization. Instead, we take a step back and try to relax the Lipschitz constraint. Theoretically, we first demonstrate a more general dual form of the Wasserstein distance called the Sobolev duality, which relaxes the Lipschitz constraint but still maintains the favorable gradient property of the Wasserstein distance. Moreover, we show that the KR duality is actually a special case of the Sobolev duality. Based on the relaxed duality, we further propose a generalized WGAN training scheme named Sobolev Wasserstein GAN (SWGAN), and empirically demonstrate the improvement of SWGAN over existing methods with extensive experiments.

Large-Scale Optimal Transport via Adversarial Training with Cycle-Consistency

Recent advances in large-scale optimal transport have greatly extended its application scenarios in machine learning. However, existing methods either not explicitly learn the transport map or do not support general cost function. In this paper, we propose an end-to-end approach for large-scale optimal transport, which directly solves the transport map and is compatible with general cost function. It models the transport map via stochastic neural networks and enforces the constraint on the marginal distributions via adversarial training. The proposed framework can be further extended towards learning Monge map or optimal bijection via adopting cycle-consistency constraint(s). We verify the effectiveness of the proposed method and demonstrate its superior performance against existing methods with large-scale real-world applications, including domain adaptation, image-to-image translation, and color transfer.

Improving Unsupervised Domain Adaptation with Variational Information Bottleneck

Domain adaptation aims to leverage the supervision signal of source domain to obtain an accurate model for target domain, where the labels are not available. To leverage and adapt the label information from source domain, most existing methods employ a feature extracting function and match the marginal distributions of source and target domains in a shared feature space. In this paper, from the perspective of information theory, we show that representation matching is actually an insufficient constraint on the feature space for obtaining a model with good generalization performance in target domain. We then propose variational bottleneck domain adaptation (VBDA), a new domain adaptation method which improves feature transferability by explicitly enforcing the feature extractor to ignore the task-irrelevant factors and focus on the information that is essential to the task of interest for both source and target domains. Extensive experimental results demonstrate that VBDA significantly outperforms state-of-the-art methods across three domain adaptation benchmark datasets.

Quantifying Exposure Bias for Neural Language Generation

The exposure bias problem refers to the training-inference discrepancy caused by teacher forcing in maximum likelihood estimation (MLE) training for recurrent neural network language models (RNNLM). It has been regarded as a central problem for natural language generation (NLG) model training. Although a lot of algorithms have been proposed to avoid teacher forcing and therefore to remove exposure bias, there is little work showing how serious the exposure bias problem is. In this work, starting from the definition of exposure bias, we propose two simple and intuitive approaches to quantify exposure bias for MLE-trained language models. Experiments are conducted on both synthetic and real data-sets. Surprisingly, our results indicate that either exposure bias is trivial (i.e. indistinguishable from the mismatch between model and data distribution), or is not as significant as it is presumed to be (with a measured performance gap of 3%). With this work, we suggest re-evaluating the viewpoint that teacher forcing or exposure bias is a major drawback of MLE training.

Triple-to-Text: Converting RDF Triples into High-Quality Natural Languages via Optimizing an Inverse KL Divergence

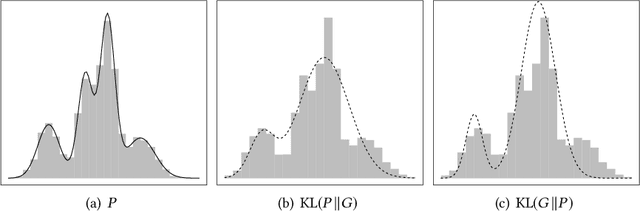
Knowledge base is one of the main forms to represent information in a structured way. A knowledge base typically consists of Resource Description Frameworks (RDF) triples which describe the entities and their relations. Generating natural language description of the knowledge base is an important task in NLP, which has been formulated as a conditional language generation task and tackled using the sequence-to-sequence framework. Current works mostly train the language models by maximum likelihood estimation, which tends to generate lousy sentences. In this paper, we argue that such a problem of maximum likelihood estimation is intrinsic, which is generally irrevocable via changing network structures. Accordingly, we propose a novel Triple-to-Text (T2T) framework, which approximately optimizes the inverse Kullback-Leibler (KL) divergence between the distributions of the real and generated sentences. Due to the nature that inverse KL imposes large penalty on fake-looking samples, the proposed method can significantly reduce the probability of generating low-quality sentences. Our experiments on three real-world datasets demonstrate that T2T can generate higher-quality sentences and outperform baseline models in several evaluation metrics.

Towards Efficient and Unbiased Implementation of Lipschitz Continuity in GANs

Lipschitz continuity recently becomes popular in generative adversarial networks (GANs). It was observed that the Lipschitz regularized discriminator leads to improved training stability and sample quality. The mainstream implementations of Lipschitz continuity include gradient penalty and spectral normalization. In this paper, we demonstrate that gradient penalty introduces undesired bias, while spectral normalization might be over restrictive. We accordingly propose a new method which is efficient and unbiased. Our experiments verify our analysis and show that the proposed method is able to achieve successful training in various situations where gradient penalty and spectral normalization fail.

Lipschitz Generative Adversarial Nets

In this paper, we study the convergence of generative adversarial networks (GANs) from the perspective of the informativeness of the gradient of the optimal discriminative function. We show that GANs without restriction on the discriminative function space commonly suffer from the problem that the gradient produced by the discriminator is uninformative to guide the generator. By contrast, Wasserstein GAN (WGAN), where the discriminative function is restricted to $1$-Lipschitz, does not suffer from such a gradient uninformativeness problem. We further show in the paper that the model with a compact dual form of Wasserstein distance, where the Lipschitz condition is relaxed, may also suffer from this issue. This implies the importance of Lipschitz condition and motivates us to study the general formulation of GANs with Lipschitz constraint, which leads to a new family of GANs that we call Lipschitz GANs (LGANs). We show that LGANs guarantee the existence and uniqueness of the optimal discriminative function as well as the existence of a unique Nash equilibrium. We prove that LGANs are generally capable of eliminating the gradient uninformativeness problem. According to our empirical analysis, LGANs are more stable and generate consistently higher quality samples compared with WGAN.