Learning to Branch in Combinatorial Optimization with Graph Pointer Networks

Branch-and-bound is a typical way to solve combinatorial optimization problems. This paper proposes a graph pointer network model for learning the variable selection policy in the branch-and-bound. We extract the graph features, global features and historical features to represent the solver state. The proposed model, which combines the graph neural network and the pointer mechanism, can effectively map from the solver state to the branching variable decisions. The model is trained to imitate the classic strong branching expert rule by a designed top-k Kullback-Leibler divergence loss function. Experiments on a series of benchmark problems demonstrate that the proposed approach significantly outperforms the widely used expert-designed branching rules. Our approach also outperforms the state-of-the-art machine-learning-based branch-and-bound methods in terms of solving speed and search tree size on all the test instances. In addition, the model can generalize to unseen instances and scale to larger instances.

Coevolutionary Framework for Generalized Multimodal Multi-objective Optimization

Most multimodal multi-objective evolutionary algorithms (MMEAs) aim to find all global Pareto optimal sets (PSs) for a multimodal multi-objective optimization problem (MMOP). However, in real-world problems, decision makers (DMs) may be also interested in local PSs. Also, searching for both global and local PSs is more general in view of dealing with MMOPs, which can be seen as a generalized MMOP. In addition, the state-of-the-art MMEAs exhibit poor convergence on high-dimension MMOPs. To address the above two issues, in this study, a novel coevolutionary framework termed CoMMEA for multimodal multi-objective optimization is proposed to better obtain both global and local PSs, and simultaneously, to improve the convergence performance in dealing with high-dimension MMOPs. Specifically, the CoMMEA introduces two archives to the search process, and coevolves them simultaneously through effective knowledge transfer. The convergence archive assists the CoMMEA to quickly approaching the Pareto optimal front (PF). The knowledge of the converged solutions is then transferred to the diversity archive which utilizes the local convergence indicator and the $\epsilon$-dominance-based method to obtain global and local PSs effectively. Experimental results show that CoMMEA is competitive compared to seven state-of-the-art MMEAs on fifty-four complex MMOPs.

Hybridization of evolutionary algorithm and deep reinforcement learning for multi-objective orienteering optimization

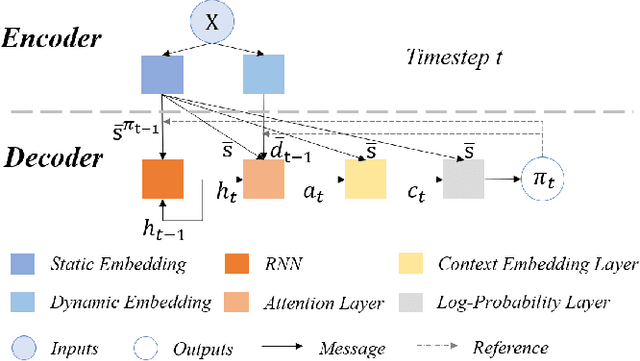
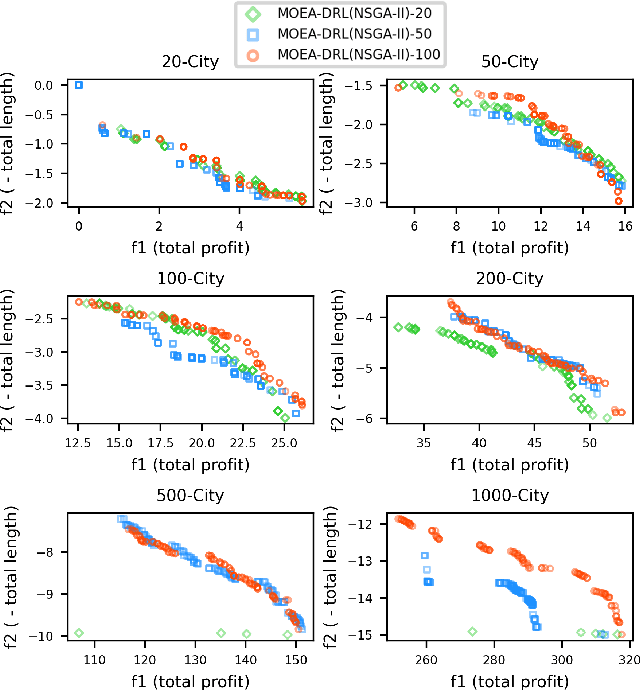
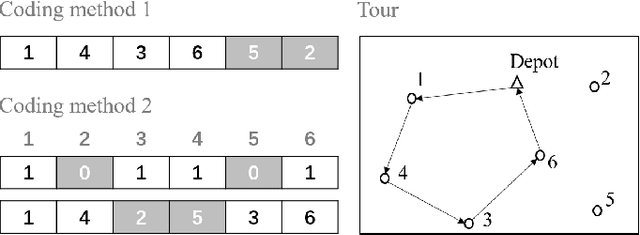
Multi-objective orienteering problems (MO-OPs) are classical multi-objective routing problems and have received a lot of attention in the past decades. This study seeks to solve MO-OPs through a problem-decomposition framework, that is, a MO-OP is decomposed into a multi-objective knapsack problem (MOKP) and a travelling salesman problem (TSP). The MOKP and TSP are then solved by a multi-objective evolutionary algorithm (MOEA) and a deep reinforcement learning (DRL) method, respectively. While the MOEA module is for selecting cities, the DRL module is for planning a Hamiltonian path for these cities. An iterative use of these two modules drives the population towards the Pareto front of MO-OPs. The effectiveness of the proposed method is compared against NSGA-II and NSGA-III on various types of MO-OP instances. Experimental results show that our method exhibits the best performance on almost all the test instances, and has shown strong generalization ability.

Deep Reinforcement Learning for Orienteering Problems Based on Decomposition

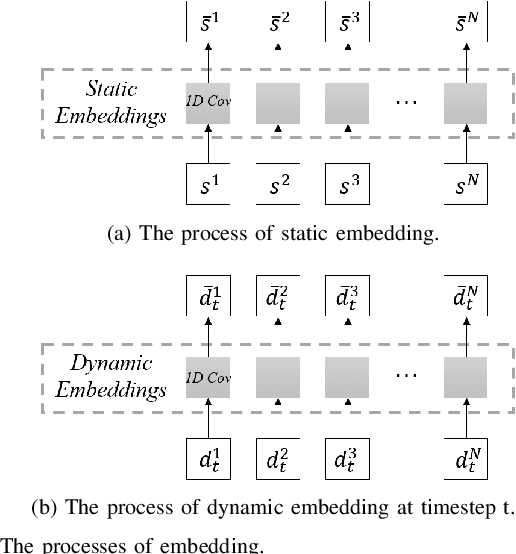
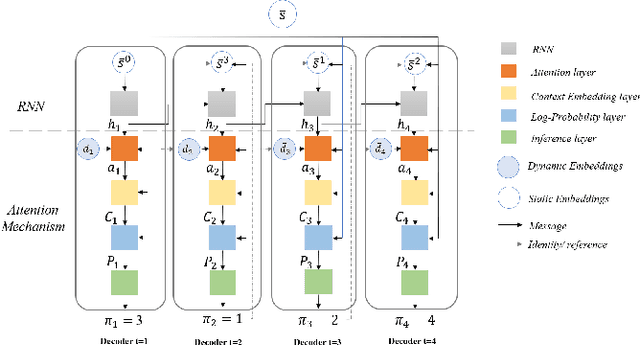
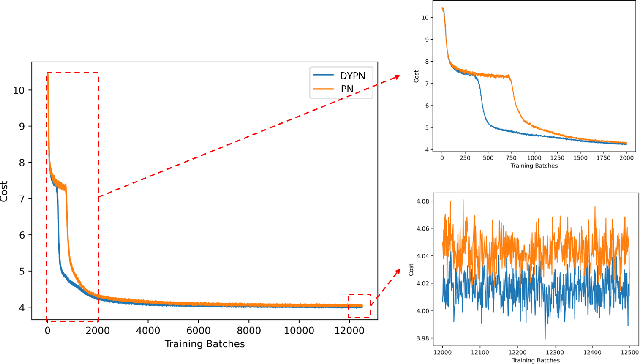
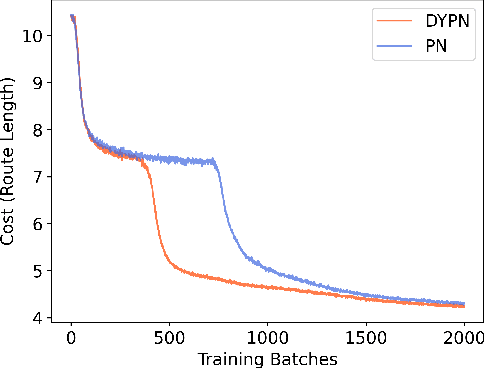
This paper presents a new method for solving an orienteering problem (OP) by breaking it down into two parts: a knapsack problem (KP) and a traveling salesman problem (TSP). A KP solver is responsible for picking nodes, while a TSP solver is responsible for designing the proper path and assisting the KP solver in judging constraint violations. To address constraints, we propose a dual-population coevolutionary algorithm (DPCA) as the KP solver, which simultaneously maintains both feasible and infeasible populations. A dynamic pointer network (DYPN) is introduced as the TSP solver, which takes city locations as inputs and immediately outputs a permutation of nodes. The model, which is trained by reinforcement learning, can capture both the structural and dynamic patterns of the given problem. The model can generalize to other instances with different scales and distributions. Experimental results show that the proposed algorithm can outperform conventional approaches in terms of training, inference, and generalization ability.

Deep Reinforcement Learning for Online Routing of Unmanned Aerial Vehicles with Wireless Power Transfer

The unmanned aerial vehicle (UAV) plays an vital role in various applications such as delivery, military mission, disaster rescue, communication, etc., due to its flexibility and versatility. This paper proposes a deep reinforcement learning method to solve the UAV online routing problem with wireless power transfer, which can charge the UAV remotely without wires, thus extending the capability of the battery-limited UAV. Our study considers the power consumption of the UAV and the wireless charging process. Unlike the previous works, we solve the problem by a designed deep neural network. The model is trained using a deep reinforcement learning method offline, and is used to optimize the UAV routing problem online. On small and large scale instances, the proposed model runs from four times to 500 times faster than Google OR-tools, the state-of-the-art combinatorial optimization solver, with identical solution quality. It also outperforms different types of heuristic and local search methods in terms of both run-time and optimality. In addition, once the model is trained, it can scale to new generated problem instances with arbitrary topology that are not seen during training. The proposed method is practically applicable when the problem scale is large and the response time is crucial.

Deep Reinforcement Learning for Combinatorial Optimization: Covering Salesman Problems

This paper introduces a new deep learning approach to approximately solve the Covering Salesman Problem (CSP). In this approach, given the city locations of a CSP as input, a deep neural network model is designed to directly output the solution. It is trained using the deep reinforcement learning without supervision. Specifically, in the model, we apply the Multi-head Attention to capture the structural patterns, and design a dynamic embedding to handle the dynamic patterns of the problem. Once the model is trained, it can generalize to various types of CSP tasks (different sizes and topologies) with no need of re-training. Through controlled experiments, the proposed approach shows desirable time complexity: it runs more than 20 times faster than the traditional heuristic solvers with a tiny gap of optimality. Moreover, it significantly outperforms the current state-of-the-art deep learning approaches for combinatorial optimization in the aspect of both training and inference. In comparison with traditional solvers, this approach is highly desirable for most of the challenging tasks in practice that are usually large-scale and require quick decisions.

Deep Reinforcement Learning for Multi-objective Optimization

This study proposes an end-to-end framework for solving multi-objective optimization problems (MOPs) using Deep Reinforcement Learning (DRL), termed DRL-MOA. The idea of decomposition is adopted to decompose a MOP into a set of scalar optimization subproblems. The subproblems are then optimized cooperatively by a neighbourhood-based parameter transfer strategy which significantly accelerates the training procedure and makes the realization of DRL-MOA possible. The subproblems are modelled as neural networks and the RL method is used to optimize them. In specific, the multi-objective travelling salesman problem (MOTSP) is solved in this work using the DRL-MOA framework by modelling the subproblem as the Pointer Network. It is found that, once the trained model is available, it can scale to MOTSPs of any number of cities, e.g., 70-city, 100-city, even the 200-city MOTSP, without re-training the model. The Pareto Front can be directly obtained by a simple feed-forward of the network; thereby, no iteration is required and the MOP can be always solved in a reasonable time. Experimental results indicate a strong convergence ability of the DRL-MOA, especially for large-scale MOTSPs, e.g., 200-city MOTSP, for which evolutionary algorithms such as NSGA-II and MOEA/D are pretty hard to converge even implemented for a large number of iterations. The DRL-MOA can also obtain a much wider spread of the PF than the two competitors. Moreover, the DRL-MOA has a high level of modularity and can be easily generalized to other MOPs by replacing the modelling of the subproblem.