Hybridization of evolutionary algorithm and deep reinforcement learning for multi-objective orienteering optimization
Paper and Code
Jun 21, 2022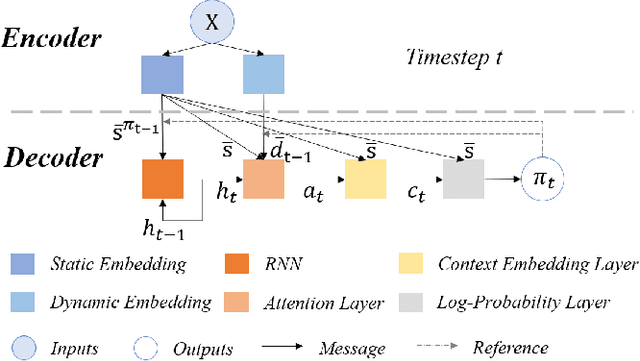
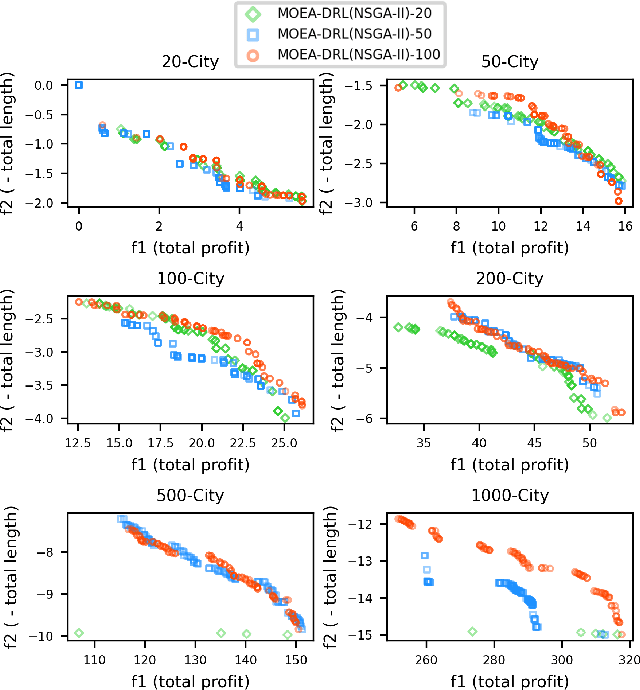
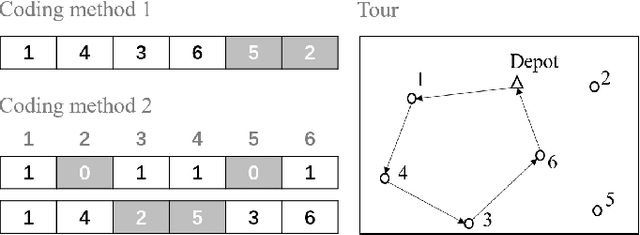
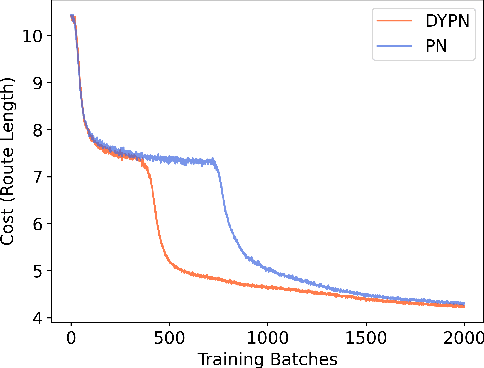
Multi-objective orienteering problems (MO-OPs) are classical multi-objective routing problems and have received a lot of attention in the past decades. This study seeks to solve MO-OPs through a problem-decomposition framework, that is, a MO-OP is decomposed into a multi-objective knapsack problem (MOKP) and a travelling salesman problem (TSP). The MOKP and TSP are then solved by a multi-objective evolutionary algorithm (MOEA) and a deep reinforcement learning (DRL) method, respectively. While the MOEA module is for selecting cities, the DRL module is for planning a Hamiltonian path for these cities. An iterative use of these two modules drives the population towards the Pareto front of MO-OPs. The effectiveness of the proposed method is compared against NSGA-II and NSGA-III on various types of MO-OP instances. Experimental results show that our method exhibits the best performance on almost all the test instances, and has shown strong generalization ability.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge