Wenhua Li
Large Language Model-assisted Meta-optimizer for Automated Design of Constrained Evolutionary Algorithm
Sep 16, 2025Abstract:Meta-black-box optimization has been significantly advanced through the use of large language models (LLMs), yet in fancy on constrained evolutionary optimization. In this work, AwesomeDE is proposed that leverages LLMs as the strategy of meta-optimizer to generate update rules for constrained evolutionary algorithm without human intervention. On the meanwhile, $RTO^2H$ framework is introduced for standardize prompt design of LLMs. The meta-optimizer is trained on a diverse set of constrained optimization problems. Key components, including prompt design and iterative refinement, are systematically analyzed to determine their impact on design quality. Experimental results demonstrate that the proposed approach outperforms existing methods in terms of computational efficiency and solution accuracy. Furthermore, AwesomeDE is shown to generalize well across distinct problem domains, suggesting its potential for broad applicability. This research contributes to the field by providing a scalable and data-driven methodology for automated constrained algorithm design, while also highlighting limitations and directions for future work.
Coevolutionary Framework for Generalized Multimodal Multi-objective Optimization
Dec 05, 2022Abstract:Most multimodal multi-objective evolutionary algorithms (MMEAs) aim to find all global Pareto optimal sets (PSs) for a multimodal multi-objective optimization problem (MMOP). However, in real-world problems, decision makers (DMs) may be also interested in local PSs. Also, searching for both global and local PSs is more general in view of dealing with MMOPs, which can be seen as a generalized MMOP. In addition, the state-of-the-art MMEAs exhibit poor convergence on high-dimension MMOPs. To address the above two issues, in this study, a novel coevolutionary framework termed CoMMEA for multimodal multi-objective optimization is proposed to better obtain both global and local PSs, and simultaneously, to improve the convergence performance in dealing with high-dimension MMOPs. Specifically, the CoMMEA introduces two archives to the search process, and coevolves them simultaneously through effective knowledge transfer. The convergence archive assists the CoMMEA to quickly approaching the Pareto optimal front (PF). The knowledge of the converged solutions is then transferred to the diversity archive which utilizes the local convergence indicator and the $\epsilon$-dominance-based method to obtain global and local PSs effectively. Experimental results show that CoMMEA is competitive compared to seven state-of-the-art MMEAs on fifty-four complex MMOPs.
Large-scale matrix optimization based multi microgrid topology design with a constrained differential evolution algorithm
Jul 18, 2022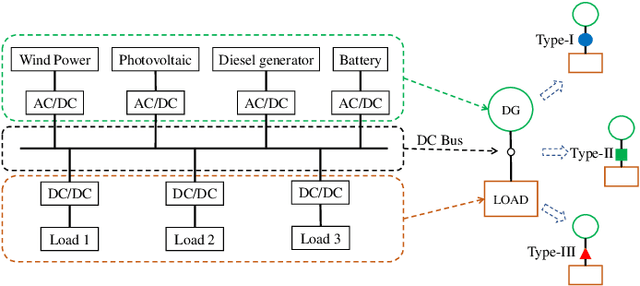
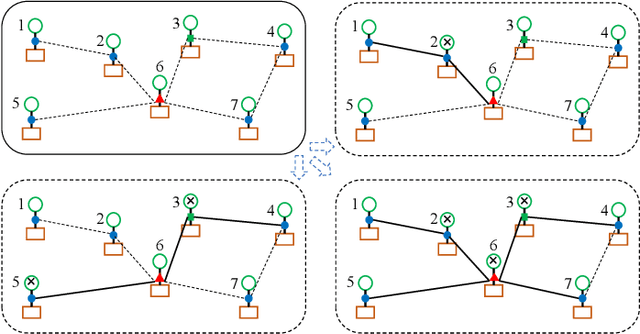
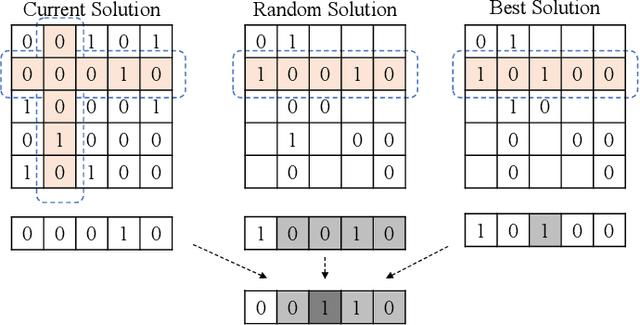
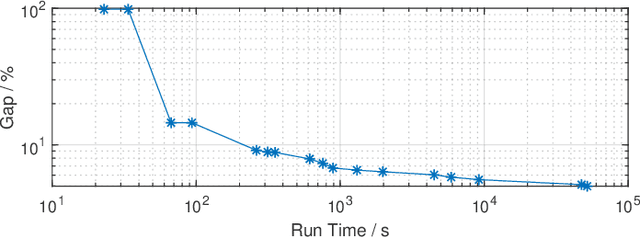
Abstract:Binary matrix optimization commonly arise in the real world, e.g., multi-microgrid network structure design problem (MGNSDP), which is to minimize the total length of the power supply line under certain constraints. Finding the global optimal solution for these problems faces a great challenge since such problems could be large-scale, sparse and multimodal. Traditional linear programming is time-consuming and cannot solve nonlinear problems. To address this issue, a novel improved feasibility rule based differential evolution algorithm, termed LBMDE, is proposed. To be specific, a general heuristic solution initialization method is first proposed to generate high-quality solutions. Then, a binary-matrix-based DE operator is introduced to produce offspring. To deal with the constraints, we proposed an improved feasibility rule based environmental selection strategy. The performance and searching behaviors of LBMDE are examined by a set of benchmark problems.
Multimodal Multi-objective Optimization: Comparative Study of the State-of-the-Art
Jul 11, 2022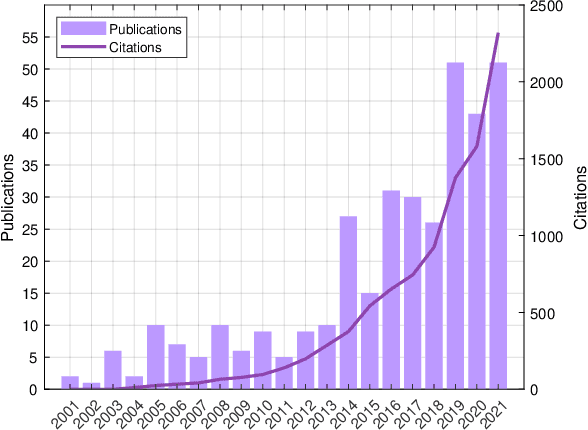
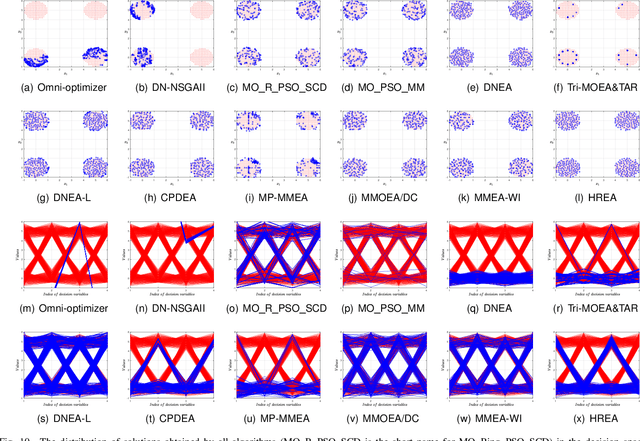
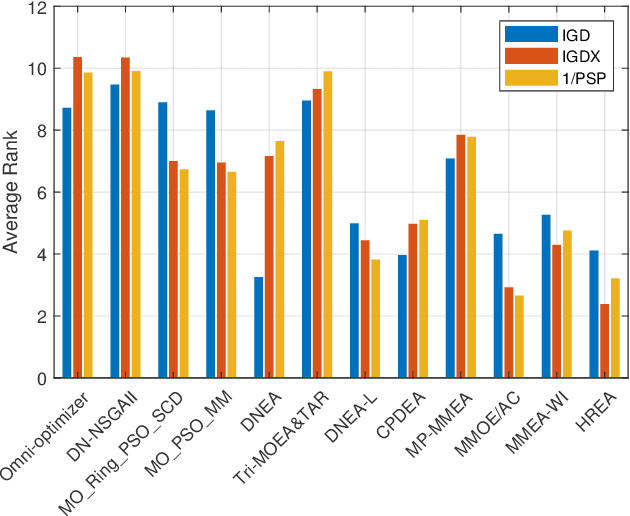
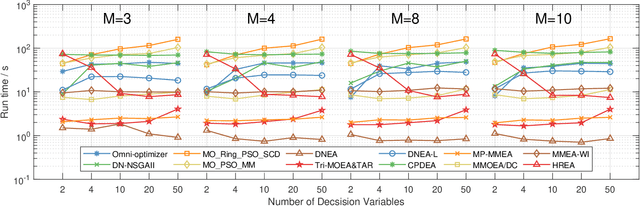
Abstract:Multimodal multi-objective problems (MMOPs) commonly arise in real-world problems where distant solutions in decision space correspond to very similar objective values. To obtain all solutions for MMOPs, many multimodal multi-objective evolutionary algorithms (MMEAs) have been proposed. For now, few studies have encompassed most of the recently proposed representative MMEAs and made a comparative comparison. In this study, we first review the related works during the last two decades. Then, we choose 12 state-of-the-art algorithms that utilize different diversity-maintaining techniques and compared their performance on existing test suites. Experimental results indicate the strengths and weaknesses of different techniques on different types of MMOPs, thus providing guidance on how to select/design MMEAs in specific scenarios.
Hybridization of evolutionary algorithm and deep reinforcement learning for multi-objective orienteering optimization
Jun 21, 2022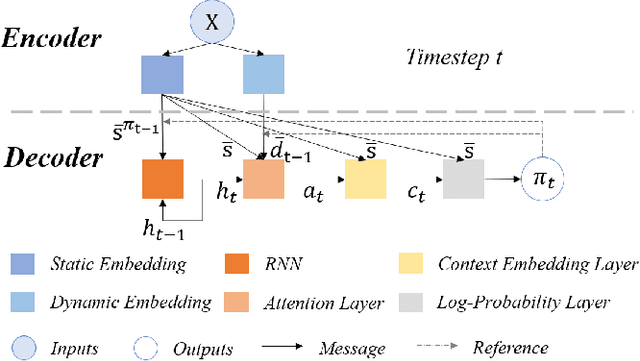
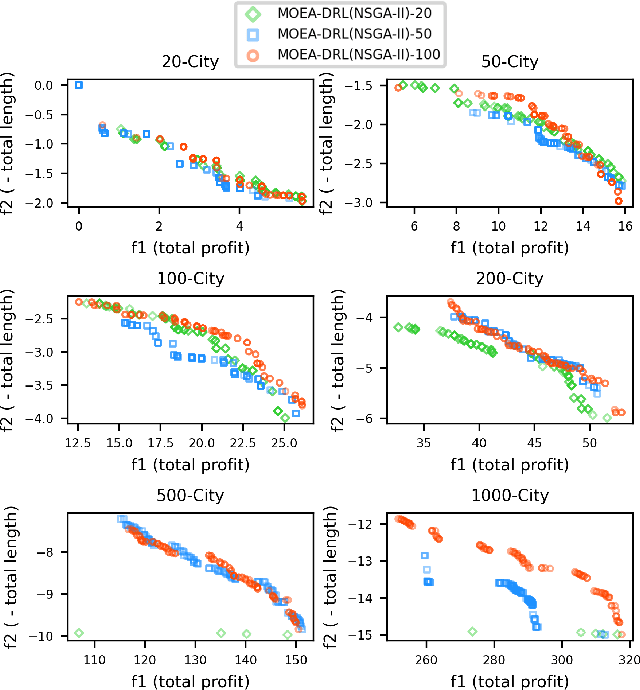
Abstract:Multi-objective orienteering problems (MO-OPs) are classical multi-objective routing problems and have received a lot of attention in the past decades. This study seeks to solve MO-OPs through a problem-decomposition framework, that is, a MO-OP is decomposed into a multi-objective knapsack problem (MOKP) and a travelling salesman problem (TSP). The MOKP and TSP are then solved by a multi-objective evolutionary algorithm (MOEA) and a deep reinforcement learning (DRL) method, respectively. While the MOEA module is for selecting cities, the DRL module is for planning a Hamiltonian path for these cities. An iterative use of these two modules drives the population towards the Pareto front of MO-OPs. The effectiveness of the proposed method is compared against NSGA-II and NSGA-III on various types of MO-OP instances. Experimental results show that our method exhibits the best performance on almost all the test instances, and has shown strong generalization ability.
Deep Reinforcement Learning for Orienteering Problems Based on Decomposition
Apr 25, 2022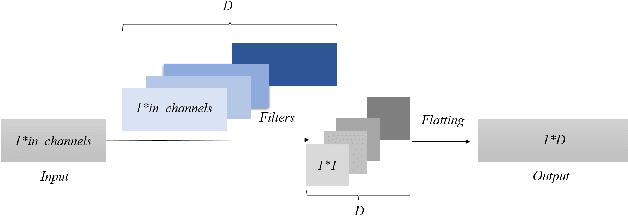
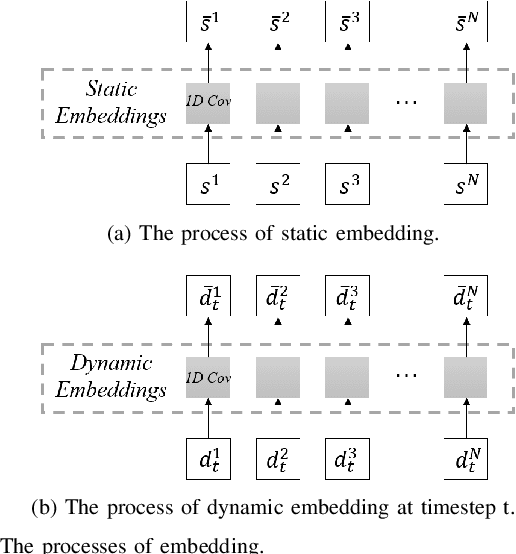
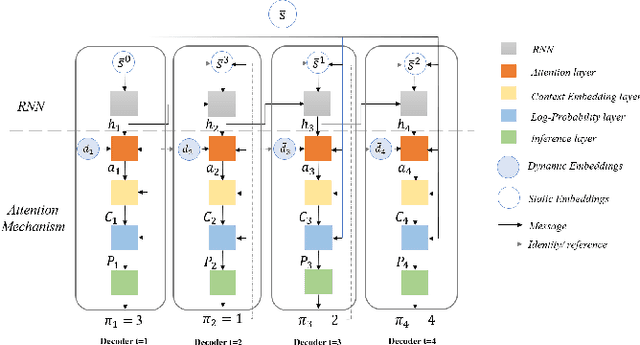
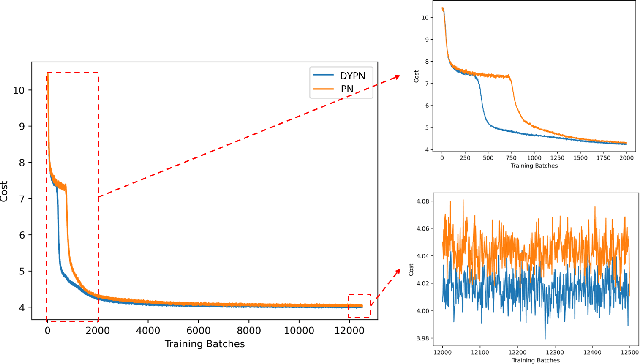
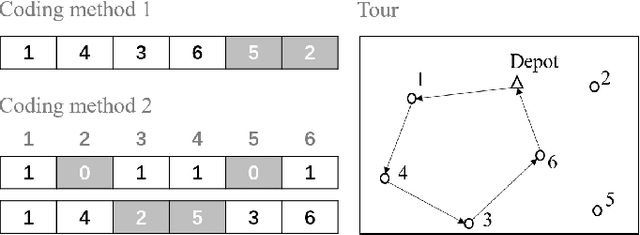
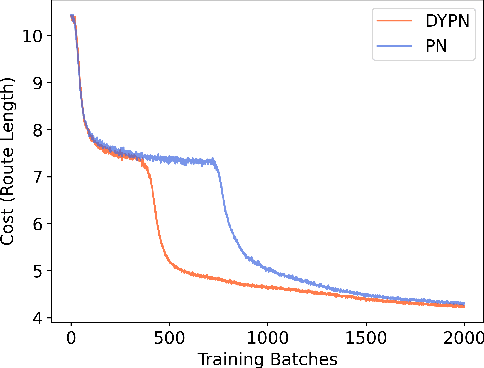
Abstract:This paper presents a new method for solving an orienteering problem (OP) by breaking it down into two parts: a knapsack problem (KP) and a traveling salesman problem (TSP). A KP solver is responsible for picking nodes, while a TSP solver is responsible for designing the proper path and assisting the KP solver in judging constraint violations. To address constraints, we propose a dual-population coevolutionary algorithm (DPCA) as the KP solver, which simultaneously maintains both feasible and infeasible populations. A dynamic pointer network (DYPN) is introduced as the TSP solver, which takes city locations as inputs and immediately outputs a permutation of nodes. The model, which is trained by reinforcement learning, can capture both the structural and dynamic patterns of the given problem. The model can generalize to other instances with different scales and distributions. Experimental results show that the proposed algorithm can outperform conventional approaches in terms of training, inference, and generalization ability.
LRA: an accelerated rough set framework based on local redundancy of attribute for feature selection
Oct 31, 2020Abstract:In this paper, we propose and prove the theorem regarding the stability of attributes in a decision system. Based on the theorem, we propose the LRA framework for accelerating rough set algorithms. It is a general-purpose framework which can be applied to almost all rough set methods significantly . Theoretical analysis guarantees high efficiency. Note that the enhancement of efficiency will not lead to any decrease of the classification accuracy. Besides, we provide a simpler prove for the positive approximation acceleration framework.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge