Inversion-DeepONet: A Novel DeepONet-Based Network with Encoder-Decoder for Full Waveform Inversion

Full waveform inversion (FWI) plays a crucial role in the field of geophysics. There has been lots of research about applying deep learning (DL) methods to FWI. The success of DL-FWI relies significantly on the quantity and diversity of the datasets. Nevertheless, existing FWI datasets, like OpenFWI, where sources have fixed locations or identical frequencies, provide limited information and do not represent the complex real-world scene. For instance, low frequencies help in resolving larger-scale structures. High frequencies allow for a more detailed subsurface features. %A single source frequency is insufficient to describe subsurface structural properties. We consider that simultaneously using sources with different frequencies, instead of performing inversion using low frequencies data and then gradually introducing higher frequencies data, has rationale and potential advantages. Hence, we develop three enhanced datasets based on OpenFWI where each source have varying locations, frequencies or both. Moreover, we propose a novel deep operator network (DeepONet) architecture Inversion-DeepONet for FWI. We utilize convolutional neural network (CNN) to extract the features from seismic data in branch net. Source parameters, such as locations and frequencies, are fed to trunk net. Then another CNN is employed as the decoder of DeepONet to reconstruct the velocity models more effectively. Through experiments, we confirm the superior performance on accuracy and generalization ability of our network, compared with existing data-driven FWI methods.

Unlocking the Power of Open Set : A New Perspective for Open-set Noisy Label Learning

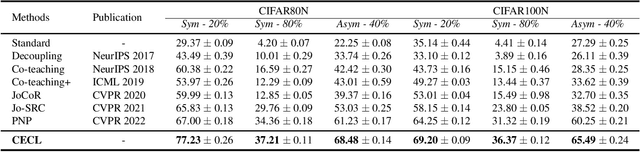
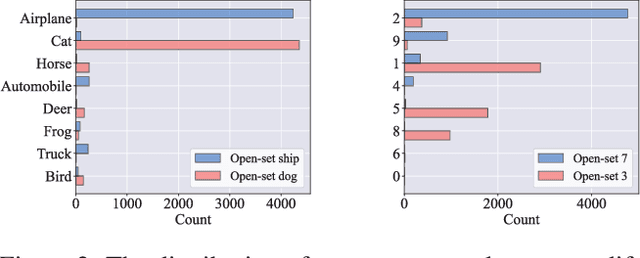
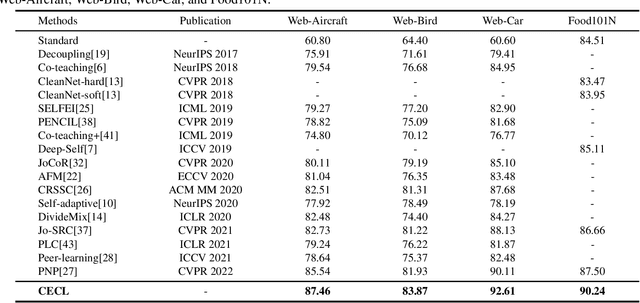
Learning from noisy data has attracted much attention, where most methods focus on closed-set label noise. However, a more common scenario in the real world is the presence of both open-set and closed-set noise. Existing methods typically identify and handle these two types of label noise separately by designing a specific strategy for each type. However, in many real-world scenarios, it would be challenging to identify open-set examples, especially when the dataset has been severely corrupted. Unlike the previous works, we explore how models behave when faced open-set examples, and find that a part of open-set examples gradually get integrated into certain known classes, which is beneficial for the seperation among known classes. Motivated by the phenomenon, in this paper, we propose a novel two-step contrastive learning method called CECL, which aims to deal with both types of label noise by exploiting the useful information of open-set examples. Specifically, we incorporate some open-set examples into closed-set classes to enhance performance while treating others as delimiters to improve representative ability. Extensive experiments on synthetic and real-world datasets with diverse label noise demonstrate that CECL can outperform state-of-the-art methods.

VI-PINNs: Variance-involved Physics-informed Neural Networks for Fast and Accurate Prediction of Partial Differential Equations

Although physics-informed neural networks(PINNs) have progressed a lot in many real applications recently, there remains problems to be further studied, such as achieving more accurate results, taking less training time, and quantifying the uncertainty of the predicted results. Recent advances in PINNs have indeed significantly improved the performance of PINNs in many aspects, but few have considered the effect of variance in the training process. In this work, we take into consideration the effect of variance and propose our VI-PINNs to give better predictions. We output two values in the final layer of the network to represent the predicted mean and variance respectively, and the latter is used to represent the uncertainty of the output. A modified negative log-likelihood loss and an auxiliary task are introduced for fast and accurate training. We perform several experiments on a wide range of different problems to highlight the advantages of our approach. The results convey that our method not only gives more accurate predictions but also converges faster.

A Survey of Learning on Small Data

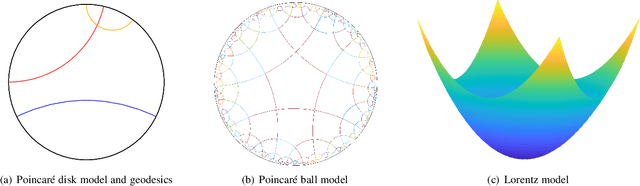
Learning on big data brings success for artificial intelligence (AI), but the annotation and training costs are expensive. In future, learning on small data is one of the ultimate purposes of AI, which requires machines to recognize objectives and scenarios relying on small data as humans. A series of machine learning models is going on this way such as active learning, few-shot learning, deep clustering. However, there are few theoretical guarantees for their generalization performance. Moreover, most of their settings are passive, that is, the label distribution is explicitly controlled by one specified sampling scenario. This survey follows the agnostic active sampling under a PAC (Probably Approximately Correct) framework to analyze the generalization error and label complexity of learning on small data using a supervised and unsupervised fashion. With these theoretical analyses, we categorize the small data learning models from two geometric perspectives: the Euclidean and non-Euclidean (hyperbolic) mean representation, where their optimization solutions are also presented and discussed. Later, some potential learning scenarios that may benefit from small data learning are then summarized, and their potential learning scenarios are also analyzed. Finally, some challenging applications such as computer vision, natural language processing that may benefit from learning on small data are also surveyed.

Large-scale matrix optimization based multi microgrid topology design with a constrained differential evolution algorithm

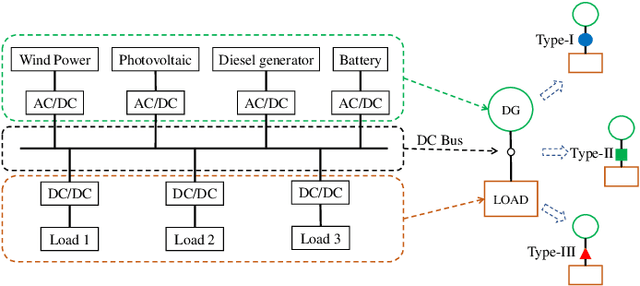
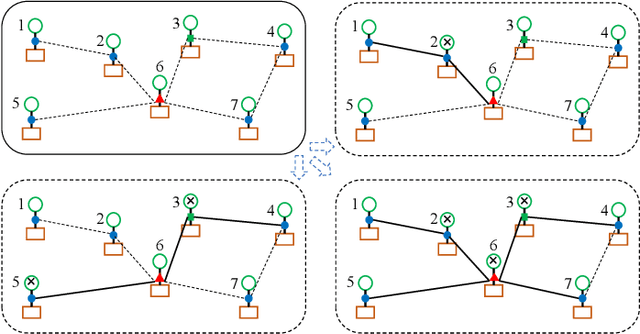
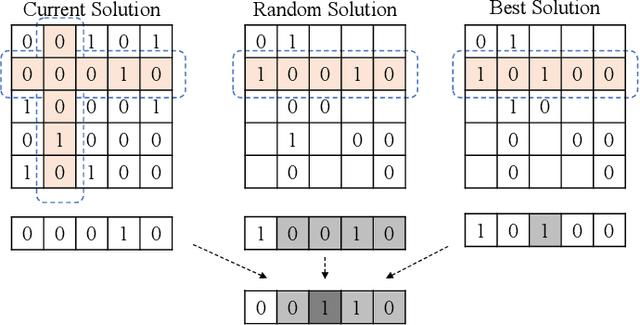
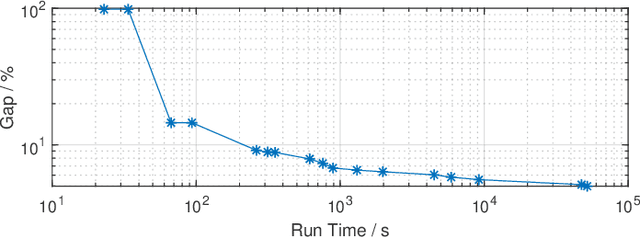
Binary matrix optimization commonly arise in the real world, e.g., multi-microgrid network structure design problem (MGNSDP), which is to minimize the total length of the power supply line under certain constraints. Finding the global optimal solution for these problems faces a great challenge since such problems could be large-scale, sparse and multimodal. Traditional linear programming is time-consuming and cannot solve nonlinear problems. To address this issue, a novel improved feasibility rule based differential evolution algorithm, termed LBMDE, is proposed. To be specific, a general heuristic solution initialization method is first proposed to generate high-quality solutions. Then, a binary-matrix-based DE operator is introduced to produce offspring. To deal with the constraints, we proposed an improved feasibility rule based environmental selection strategy. The performance and searching behaviors of LBMDE are examined by a set of benchmark problems.