Yaming Guo
Investigating Out-of-Distribution Generalization of GNNs: An Architecture Perspective
Feb 14, 2024Abstract:Graph neural networks (GNNs) have exhibited remarkable performance under the assumption that test data comes from the same distribution of training data. However, in real-world scenarios, this assumption may not always be valid. Consequently, there is a growing focus on exploring the Out-of-Distribution (OOD) problem in the context of graphs. Most existing efforts have primarily concentrated on improving graph OOD generalization from two \textbf{model-agnostic} perspectives: data-driven methods and strategy-based learning. However, there has been limited attention dedicated to investigating the impact of well-known \textbf{GNN model architectures} on graph OOD generalization, which is orthogonal to existing research. In this work, we provide the first comprehensive investigation of OOD generalization on graphs from an architecture perspective, by examining the common building blocks of modern GNNs. Through extensive experiments, we reveal that both the graph self-attention mechanism and the decoupled architecture contribute positively to graph OOD generalization. In contrast, we observe that the linear classification layer tends to compromise graph OOD generalization capability. Furthermore, we provide in-depth theoretical insights and discussions to underpin these discoveries. These insights have empowered us to develop a novel GNN backbone model, DGAT, designed to harness the robust properties of both graph self-attention mechanism and the decoupled architecture. Extensive experimental results demonstrate the effectiveness of our model under graph OOD, exhibiting substantial and consistent enhancements across various training strategies.
A Survey of Learning on Small Data
Jul 29, 2022


Abstract:Learning on big data brings success for artificial intelligence (AI), but the annotation and training costs are expensive. In future, learning on small data is one of the ultimate purposes of AI, which requires machines to recognize objectives and scenarios relying on small data as humans. A series of machine learning models is going on this way such as active learning, few-shot learning, deep clustering. However, there are few theoretical guarantees for their generalization performance. Moreover, most of their settings are passive, that is, the label distribution is explicitly controlled by one specified sampling scenario. This survey follows the agnostic active sampling under a PAC (Probably Approximately Correct) framework to analyze the generalization error and label complexity of learning on small data using a supervised and unsupervised fashion. With these theoretical analyses, we categorize the small data learning models from two geometric perspectives: the Euclidean and non-Euclidean (hyperbolic) mean representation, where their optimization solutions are also presented and discussed. Later, some potential learning scenarios that may benefit from small data learning are then summarized, and their potential learning scenarios are also analyzed. Finally, some challenging applications such as computer vision, natural language processing that may benefit from learning on small data are also surveyed.
When an Active Learner Meets a Black-box Teacher
Jun 30, 2022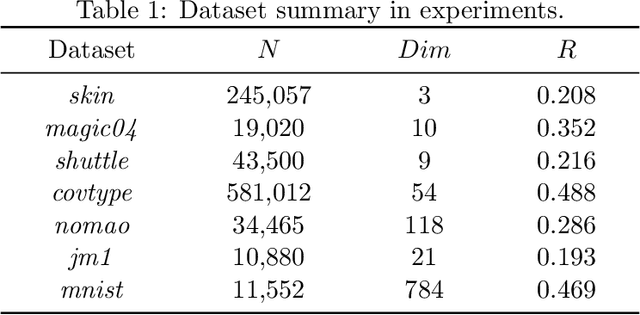
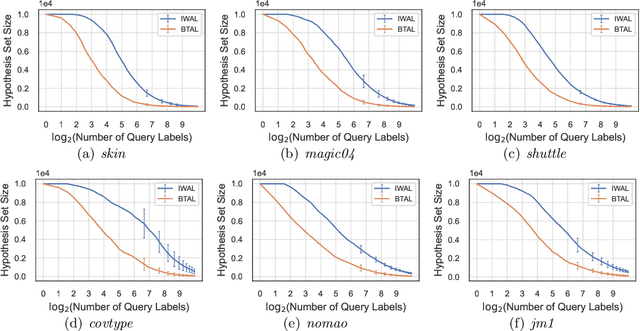
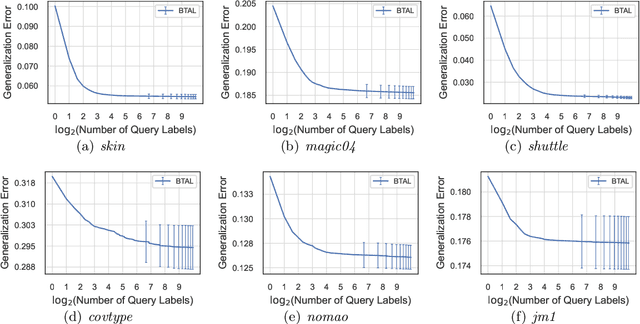
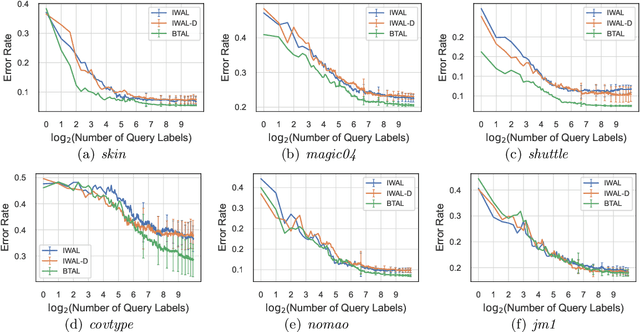
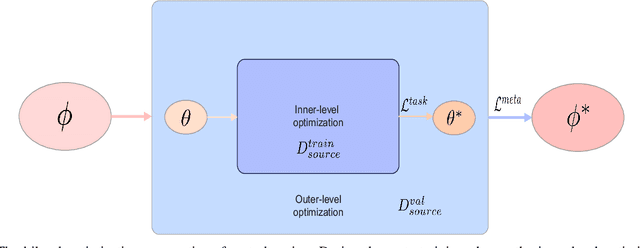
Abstract:Active learning maximizes the hypothesis updates to find those desired unlabeled data. An inherent assumption is that this learning manner can derive those updates into the optimal hypothesis. However, its convergence may not be guaranteed well if those incremental updates are negative and disordered. In this paper, we introduce a machine teacher who provides a black-box teaching hypothesis for an active learner, where the teaching hypothesis is an effective approximation for the optimal hypothesis. Theoretically, we prove that, under the guidance of this teaching hypothesis, the learner can converge into a tighter generalization error and label complexity bound than those non-educated learners who do not receive any guidance from a teacher. We further consider two teaching scenarios: teaching a white-box and black-box learner, where self-improvement of teaching is firstly proposed to improve the teaching performance. Experiments verify this idea and show better performance than the fundamental active learning strategies, such as IWAL, IWAL-D, etc.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge