When an Active Learner Meets a Black-box Teacher

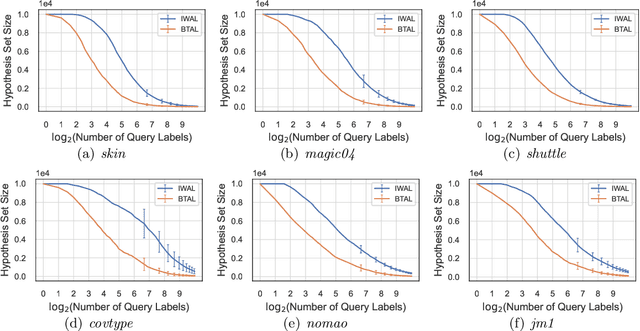
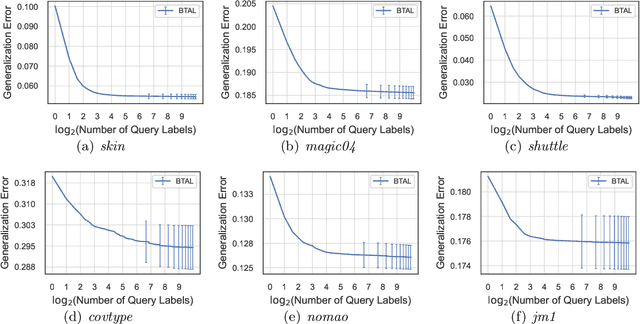
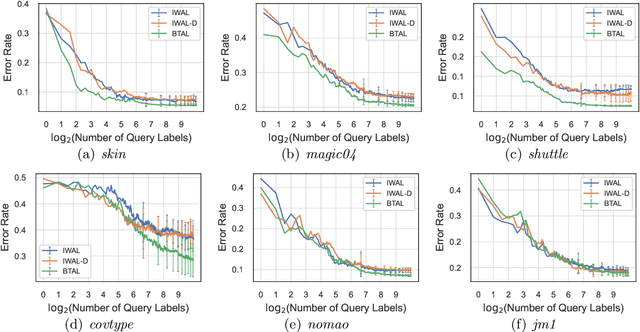
Active learning maximizes the hypothesis updates to find those desired unlabeled data. An inherent assumption is that this learning manner can derive those updates into the optimal hypothesis. However, its convergence may not be guaranteed well if those incremental updates are negative and disordered. In this paper, we introduce a machine teacher who provides a black-box teaching hypothesis for an active learner, where the teaching hypothesis is an effective approximation for the optimal hypothesis. Theoretically, we prove that, under the guidance of this teaching hypothesis, the learner can converge into a tighter generalization error and label complexity bound than those non-educated learners who do not receive any guidance from a teacher. We further consider two teaching scenarios: teaching a white-box and black-box learner, where self-improvement of teaching is firstly proposed to improve the teaching performance. Experiments verify this idea and show better performance than the fundamental active learning strategies, such as IWAL, IWAL-D, etc.