The RoboSense Challenge: Sense Anything, Navigate Anywhere, Adapt Across Platforms

Autonomous systems are increasingly deployed in open and dynamic environments -- from city streets to aerial and indoor spaces -- where perception models must remain reliable under sensor noise, environmental variation, and platform shifts. However, even state-of-the-art methods often degrade under unseen conditions, highlighting the need for robust and generalizable robot sensing. The RoboSense 2025 Challenge is designed to advance robustness and adaptability in robot perception across diverse sensing scenarios. It unifies five complementary research tracks spanning language-grounded decision making, socially compliant navigation, sensor configuration generalization, cross-view and cross-modal correspondence, and cross-platform 3D perception. Together, these tasks form a comprehensive benchmark for evaluating real-world sensing reliability under domain shifts, sensor failures, and platform discrepancies. RoboSense 2025 provides standardized datasets, baseline models, and unified evaluation protocols, enabling large-scale and reproducible comparison of robust perception methods. The challenge attracted 143 teams from 85 institutions across 16 countries, reflecting broad community engagement. By consolidating insights from 23 winning solutions, this report highlights emerging methodological trends, shared design principles, and open challenges across all tracks, marking a step toward building robots that can sense reliably, act robustly, and adapt across platforms in real-world environments.

Mass Concept Erasure in Diffusion Models with Concept Hierarchy

The success of diffusion models has raised concerns about the generation of unsafe or harmful content, prompting concept erasure approaches that fine-tune modules to suppress specific concepts while preserving general generative capabilities. However, as the number of erased concepts grows, these methods often become inefficient and ineffective, since each concept requires a separate set of fine-tuned parameters and may degrade the overall generation quality. In this work, we propose a supertype-subtype concept hierarchy that organizes erased concepts into a parent-child structure. Each erased concept is treated as a child node, and semantically related concepts (e.g., macaw, and bald eagle) are grouped under a shared parent node, referred to as a supertype concept (e.g., bird). Rather than erasing concepts individually, we introduce an effective and efficient group-wise suppression method, where semantically similar concepts are grouped and erased jointly by sharing a single set of learnable parameters. During the erasure phase, standard diffusion regularization is applied to preserve denoising process in unmasked regions. To mitigate the degradation of supertype generation caused by excessive erasure of semantically related subtypes, we propose a novel method called Supertype-Preserving Low-Rank Adaptation (SuPLoRA), which encodes the supertype concept information in the frozen down-projection matrix and updates only the up-projection matrix during erasure. Theoretical analysis demonstrates the effectiveness of SuPLoRA in mitigating generation performance degradation. We construct a more challenging benchmark that requires simultaneous erasure of concepts across diverse domains, including celebrities, objects, and pornographic content.

DGSAN: Dual-Graph Spatiotemporal Attention Network for Pulmonary Nodule Malignancy Prediction

Lung cancer continues to be the leading cause of cancer-related deaths globally. Early detection and diagnosis of pulmonary nodules are essential for improving patient survival rates. Although previous research has integrated multimodal and multi-temporal information, outperforming single modality and single time point, the fusion methods are limited to inefficient vector concatenation and simple mutual attention, highlighting the need for more effective multimodal information fusion. To address these challenges, we introduce a Dual-Graph Spatiotemporal Attention Network, which leverages temporal variations and multimodal data to enhance the accuracy of predictions. Our methodology involves developing a Global-Local Feature Encoder to better capture the local, global, and fused characteristics of pulmonary nodules. Additionally, a Dual-Graph Construction method organizes multimodal features into inter-modal and intra-modal graphs. Furthermore, a Hierarchical Cross-Modal Graph Fusion Module is introduced to refine feature integration. We also compiled a novel multimodal dataset named the NLST-cmst dataset as a comprehensive source of support for related research. Our extensive experiments, conducted on both the NLST-cmst and curated CSTL-derived datasets, demonstrate that our DGSAN significantly outperforms state-of-the-art methods in classifying pulmonary nodules with exceptional computational efficiency.

Driving in Corner Case: A Real-World Adversarial Closed-Loop Evaluation Platform for End-to-End Autonomous Driving

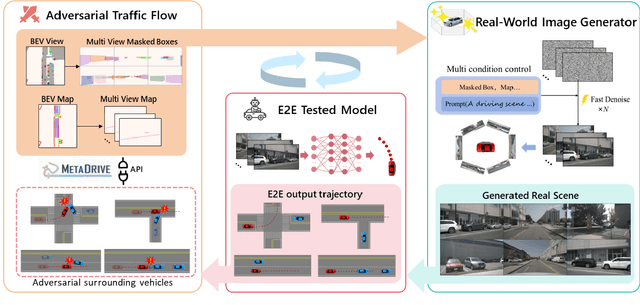
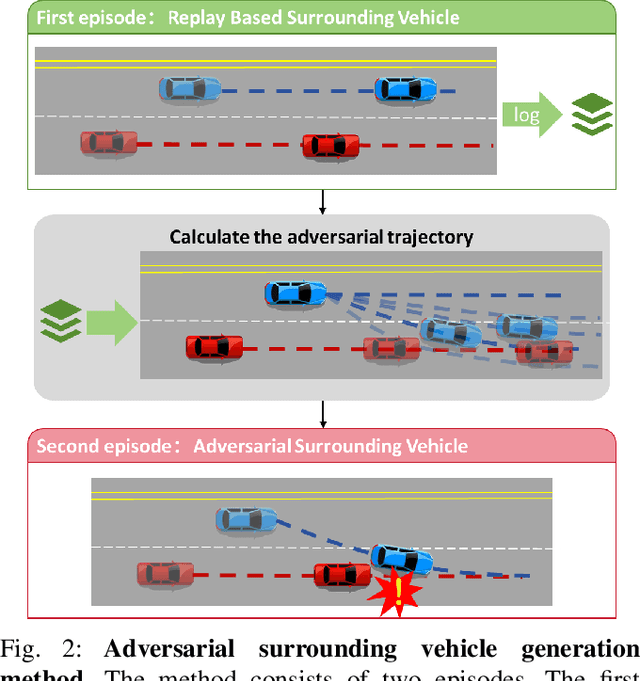
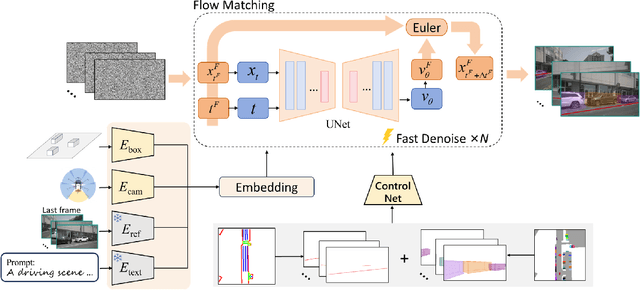
Safety-critical corner cases, difficult to collect in the real world, are crucial for evaluating end-to-end autonomous driving. Adversarial interaction is an effective method to generate such safety-critical corner cases. While existing adversarial evaluation methods are built for models operating in simplified simulation environments, adversarial evaluation for real-world end-to-end autonomous driving has been little explored. To address this challenge, we propose a closed-loop evaluation platform for end-to-end autonomous driving, which can generate adversarial interactions in real-world scenes. In our platform, the real-world image generator cooperates with an adversarial traffic policy to evaluate various end-to-end models trained on real-world data. The generator, based on flow matching, efficiently and stably generates real-world images according to the traffic environment information. The efficient adversarial surrounding vehicle policy is designed to model challenging interactions and create corner cases that current autonomous driving systems struggle to handle. Experimental results demonstrate that the platform can generate realistic driving images efficiently. Through evaluating the end-to-end models such as UniAD and VAD, we demonstrate that based on the adversarial policy, our platform evaluates the performance degradation of the tested model in corner cases. This result indicates that this platform can effectively detect the model's potential issues, which will facilitate the safety and robustness of end-to-end autonomous driving.

Noise-robust Contrastive Learning for Critical Transition Detection in Dynamical Systems

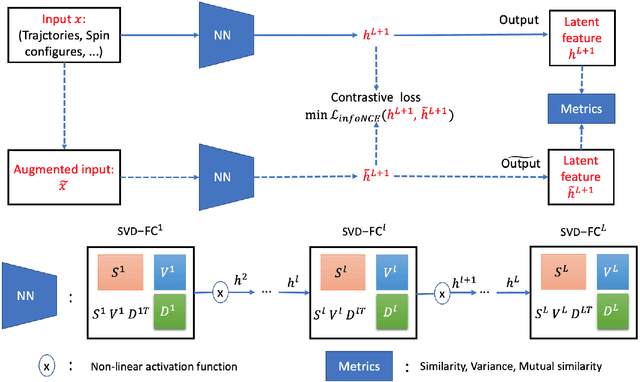
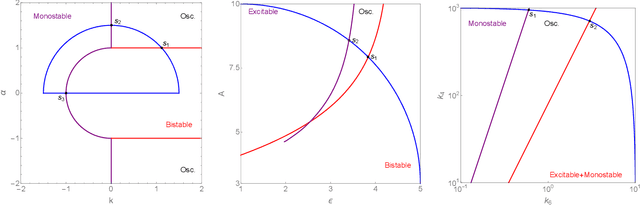
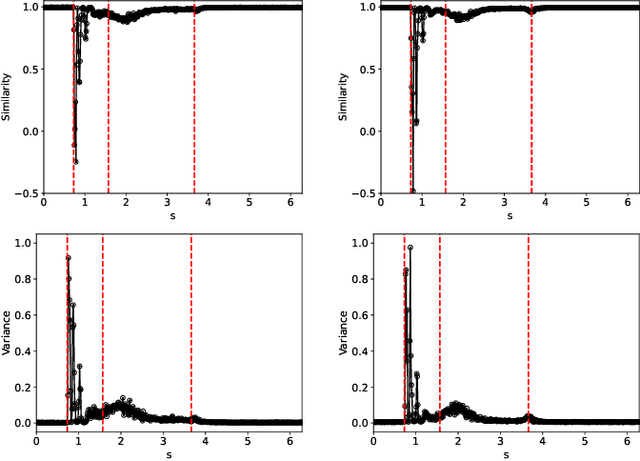
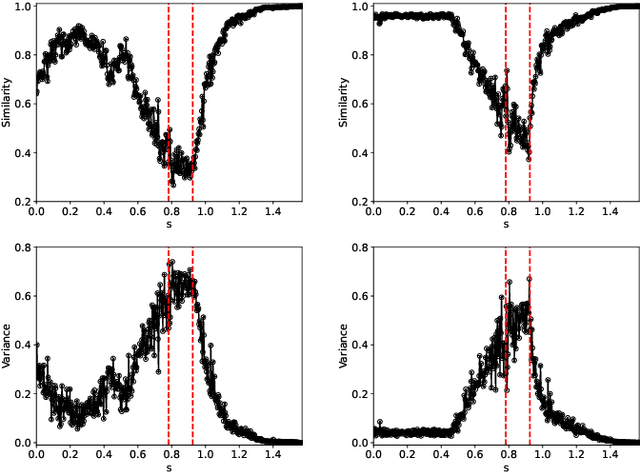
Detecting critical transitions in complex, noisy time-series data is a fundamental challenge across science and engineering. Such transitions may be anticipated by the emergence of a low-dimensional order parameter, whose signature is often masked by high-amplitude stochastic variability. Standard contrastive learning approaches based on deep neural networks, while promising for detecting critical transitions, are often overparameterized and sensitive to irrelevant noise, leading to inaccurate identification of critical points. To address these limitations, we propose a neural network architecture, constructed using singular value decomposition technique, together with a strictly semi-orthogonality-constrained training algorithm, to enhance the performance of traditional contrastive learning. Extensive experiments demonstrate that the proposed method matches the performance of traditional contrastive learning techniques in identifying critical transitions, yet is considerably more lightweight and markedly more resistant to noise.

TS-DP: Reinforcement Speculative Decoding For Temporal Adaptive Diffusion Policy Acceleration

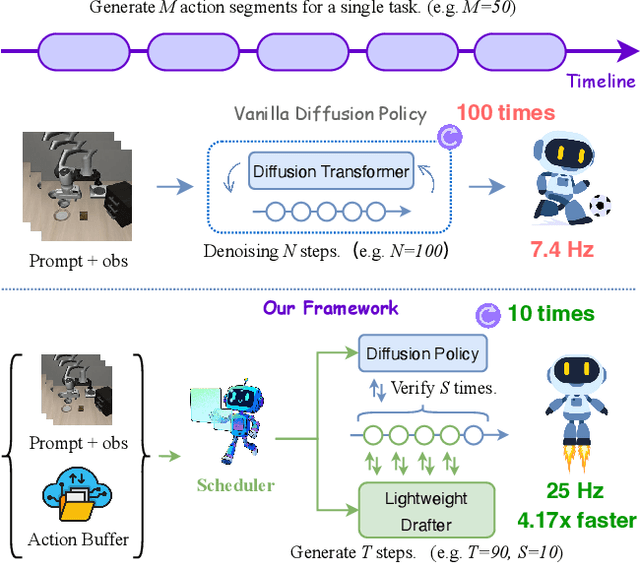
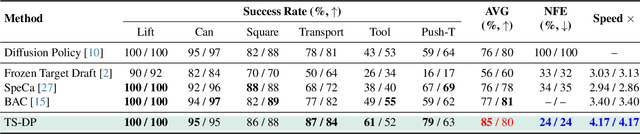
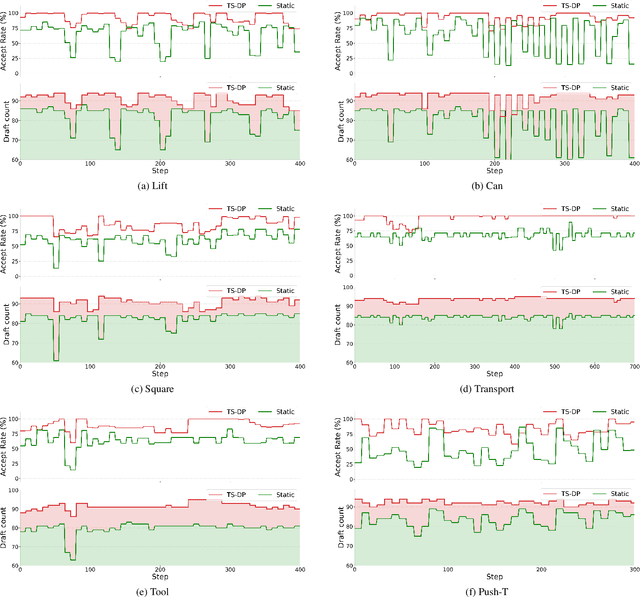
Diffusion Policy (DP) excels in embodied control but suffers from high inference latency and computational cost due to multiple iterative denoising steps. The temporal complexity of embodied tasks demands a dynamic and adaptable computation mode. Static and lossy acceleration methods, such as quantization, fail to handle such dynamic embodied tasks, while speculative decoding offers a lossless and adaptive yet underexplored alternative for DP. However, it is non-trivial to address the following challenges: how to match the base model's denoising quality at lower cost under time-varying task difficulty in embodied settings, and how to dynamically and interactively adjust computation based on task difficulty in such environments. In this paper, we propose Temporal-aware Reinforcement-based Speculative Diffusion Policy (TS-DP), the first framework that enables speculative decoding for DP with temporal adaptivity. First, to handle dynamic environments where task difficulty varies over time, we distill a Transformer-based drafter to imitate the base model and replace its costly denoising calls. Second, an RL-based scheduler further adapts to time-varying task difficulty by adjusting speculative parameters to maintain accuracy while improving efficiency. Extensive experiments across diverse embodied environments demonstrate that TS-DP achieves up to 4.17 times faster inference with over 94% accepted drafts, reaching an inference frequency of 25 Hz and enabling real-time diffusion-based control without performance degradation.

VVS: Accelerating Speculative Decoding for Visual Autoregressive Generation via Partial Verification Skipping

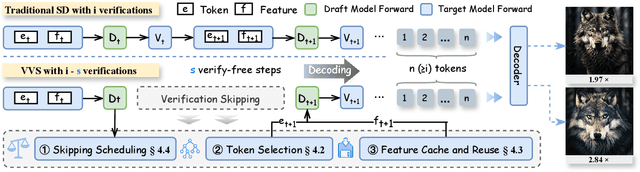
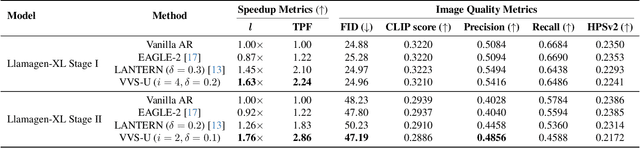
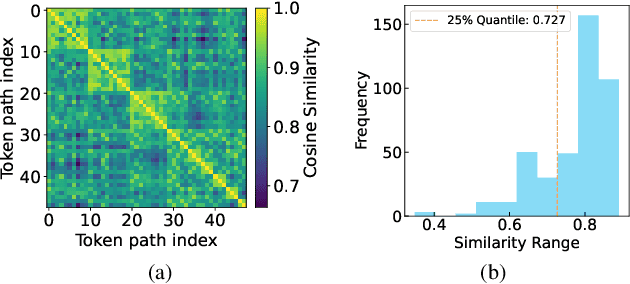
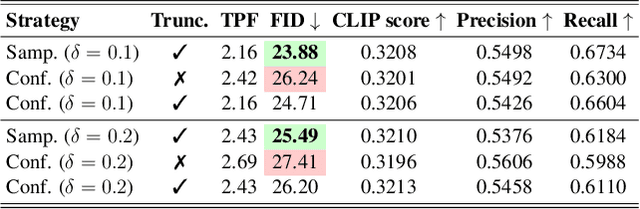
Visual autoregressive (AR) generation models have demonstrated strong potential for image generation, yet their next-token-prediction paradigm introduces considerable inference latency. Although speculative decoding (SD) has been proven effective for accelerating visual AR models, its "draft one step, then verify one step" paradigm prevents a direct reduction of the forward passes, thus restricting acceleration potential. Motivated by the visual token interchangeability, we for the first time to explore verification skipping in the SD process of visual AR model generation to explicitly cut the number of target model forward passes, thereby reducing inference latency. Based on an analysis of the drafting stage's characteristics, we observe that verification redundancy and stale feature reusability are key factors to retain generation quality and speedup for verification-free steps. Inspired by these two observations, we propose a novel SD framework VVS to accelerate visual AR generation via partial verification skipping, which integrates three complementary modules: (1) a verification-free token selector with dynamical truncation, (2) token-level feature caching and reuse, and (3) fine-grained skipped step scheduling. Consequently, VVS reduces the number of target model forward passes by a factor of $2.8\times$ relative to vanilla AR decoding while maintaining competitive generation quality, offering a superior speed-quality trade-off over conventional SD frameworks and revealing strong potential to reshape the SD paradigm.

Connectivity-Guided Sparsification of 2-FWL GNNs: Preserving Full Expressivity with Improved Efficiency

Higher-order Graph Neural Networks (HOGNNs) based on the 2-FWL test achieve superior expressivity by modeling 2- and 3-node interactions, but at $\mathcal{O}(n^3)$ computational cost. However, this computational burden is typically mitigated by existing efficiency methods at the cost of reduced expressivity. We propose \textbf{Co-Sparsify}, a connectivity-aware sparsification framework that eliminates \emph{provably redundant} computations while preserving full 2-FWL expressive power. Our key insight is that 3-node interactions are expressively necessary only within \emph{biconnected components} -- maximal subgraphs where every pair of nodes lies on a cycle. Outside these components, structural relationships can be fully captured via 2-node message passing or global readout, rendering higher-order modeling unnecessary. Co-Sparsify restricts 2-node message passing to connected components and 3-node interactions to biconnected ones, removing computation without approximation or sampling. We prove that Co-Sparsified GNNs are as expressive as the 2-FWL test. Empirically, on PPGN, Co-Sparsify matches or exceeds accuracy on synthetic substructure counting tasks and achieves state-of-the-art performance on real-world benchmarks (ZINC, QM9). This study demonstrates that high expressivity and scalability are not mutually exclusive: principled, topology-guided sparsification enables powerful, efficient GNNs with theoretical guarantees.

Unified Humanoid Fall-Safety Policy from a Few Demonstrations

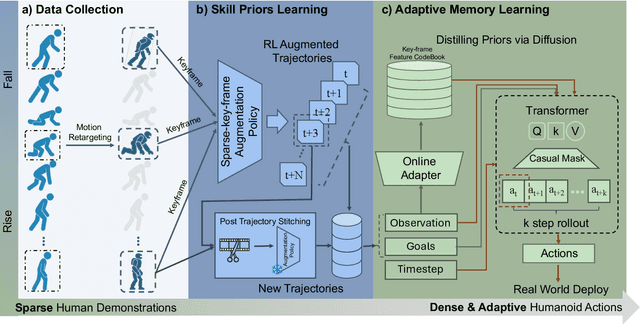
Falling is an inherent risk of humanoid mobility. Maintaining stability is thus a primary safety focus in robot control and learning, yet no existing approach fully averts loss of balance. When instability does occur, prior work addresses only isolated aspects of falling: avoiding falls, choreographing a controlled descent, or standing up afterward. Consequently, humanoid robots lack integrated strategies for impact mitigation and prompt recovery when real falls defy these scripts. We aim to go beyond keeping balance to make the entire fall-and-recovery process safe and autonomous: prevent falls when possible, reduce impact when unavoidable, and stand up when fallen. By fusing sparse human demonstrations with reinforcement learning and an adaptive diffusion-based memory of safe reactions, we learn adaptive whole-body behaviors that unify fall prevention, impact mitigation, and rapid recovery in one policy. Experiments in simulation and on a Unitree G1 demonstrate robust sim-to-real transfer, lower impact forces, and consistently fast recovery across diverse disturbances, pointing towards safer, more resilient humanoids in real environments. Videos are available at https://firm2025.github.io/.

Maritime Communication in Evaporation Duct Environment with Ship Trajectory Optimization

In maritime wireless networks, the evaporation duct effect has been known as a preferable condition for long-range transmissions. However, how to effectively utilize the duct effect for efficient communication design is still open for investigation. In this paper, we consider a typical scenario of ship-to-shore data transmission, where a ship collects data from multiple oceanographic buoys, sails from one to another, and transmits the collected data back to a terrestrial base station during its voyage. A novel framework, which exploits priori information of the channel gain map in the presence of evaporation duct, is proposed to minimize the data transmission time and the sailing time by optimizing the ship's trajectory. To this end, a multi-objective optimization problem is formulated and is further solved by a dynamic population PSO-integrated NSGA-II algorithm. Through simulations, it is demonstrated that, compared to the benchmark scheme which ignores useful information of the evaporation duct, the proposed scheme can effectively reduce both the data transmission time and the sailing time.