Seedance 1.5 pro: A Native Audio-Visual Joint Generation Foundation Model

Recent strides in video generation have paved the way for unified audio-visual generation. In this work, we present Seedance 1.5 pro, a foundational model engineered specifically for native, joint audio-video generation. Leveraging a dual-branch Diffusion Transformer architecture, the model integrates a cross-modal joint module with a specialized multi-stage data pipeline, achieving exceptional audio-visual synchronization and superior generation quality. To ensure practical utility, we implement meticulous post-training optimizations, including Supervised Fine-Tuning (SFT) on high-quality datasets and Reinforcement Learning from Human Feedback (RLHF) with multi-dimensional reward models. Furthermore, we introduce an acceleration framework that boosts inference speed by over 10X. Seedance 1.5 pro distinguishes itself through precise multilingual and dialect lip-syncing, dynamic cinematic camera control, and enhanced narrative coherence, positioning it as a robust engine for professional-grade content creation. Seedance 1.5 pro is now accessible on Volcano Engine at https://console.volcengine.com/ark/region:ark+cn-beijing/experience/vision?type=GenVideo.

Let the Model Learn to Feel: Mode-Guided Tonality Injection for Symbolic Music Emotion Recognition

Music emotion recognition is a key task in symbolic music understanding (SMER). Recent approaches have shown promising results by fine-tuning large-scale pre-trained models (e.g., MIDIBERT, a benchmark in symbolic music understanding) to map musical semantics to emotional labels. While these models effectively capture distributional musical semantics, they often overlook tonal structures, particularly musical modes, which play a critical role in emotional perception according to music psychology. In this paper, we investigate the representational capacity of MIDIBERT and identify its limitations in capturing mode-emotion associations. To address this issue, we propose a Mode-Guided Enhancement (MoGE) strategy that incorporates psychological insights on mode into the model. Specifically, we first conduct a mode augmentation analysis, which reveals that MIDIBERT fails to effectively encode emotion-mode correlations. We then identify the least emotion-relevant layer within MIDIBERT and introduce a Mode-guided Feature-wise linear modulation injection (MoFi) framework to inject explicit mode features, thereby enhancing the model's capability in emotional representation and inference. Extensive experiments on the EMOPIA and VGMIDI datasets demonstrate that our mode injection strategy significantly improves SMER performance, achieving accuracies of 75.2% and 59.1%, respectively. These results validate the effectiveness of mode-guided modeling in symbolic music emotion recognition.

Robust Variational Model Based Tailored UNet: Leveraging Edge Detector and Mean Curvature for Improved Image Segmentation

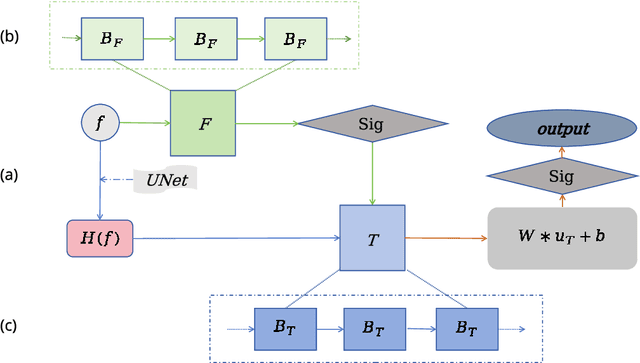
To address the challenge of segmenting noisy images with blurred or fragmented boundaries, this paper presents a robust version of Variational Model Based Tailored UNet (VM_TUNet), a hybrid framework that integrates variational methods with deep learning. The proposed approach incorporates physical priors, an edge detector and a mean curvature term, into a modified Cahn-Hilliard equation, aiming to combine the interpretability and boundary-smoothing advantages of variational partial differential equations (PDEs) with the strong representational ability of deep neural networks. The architecture consists of two collaborative modules: an F module, which conducts efficient frequency domain preprocessing to alleviate poor local minima, and a T module, which ensures accurate and stable local computations, backed by a stability estimate. Extensive experiments on three benchmark datasets indicate that the proposed method achieves a balanced trade-off between performance and computational efficiency, which yields competitive quantitative results and improved visual quality compared to pure convolutional neural network (CNN) based models, while achieving performance close to that of transformer-based method with reasonable computational expense.

The Role of Rank in Mismatched Low-Rank Symmetric Matrix Estimation

We investigate the performance of a Bayesian statistician tasked with recovering a rank-\(k\) signal matrix \(\bS \bS^{\top} \in \mathbb{R}^{n \times n}\), corrupted by element-wise additive Gaussian noise. This problem lies at the core of numerous applications in machine learning, signal processing, and statistics. We derive an analytic expression for the asymptotic mean-square error (MSE) of the Bayesian estimator under mismatches in the assumed signal rank, signal power, and signal-to-noise ratio (SNR), considering both sphere and Gaussian signals. Additionally, we conduct a rigorous analysis of how rank mismatch influences the asymptotic MSE. Our primary technical tools include the spectrum of Gaussian orthogonal ensembles (GOE) with low-rank perturbations and asymptotic behavior of \(k\)-dimensional spherical integrals.

Decoupling Classifier for Boosting Few-shot Object Detection and Instance Segmentation

This paper focus on few-shot object detection~(FSOD) and instance segmentation~(FSIS), which requires a model to quickly adapt to novel classes with a few labeled instances. The existing methods severely suffer from bias classification because of the missing label issue which naturally exists in an instance-level few-shot scenario and is first formally proposed by us. Our analysis suggests that the standard classification head of most FSOD or FSIS models needs to be decoupled to mitigate the bias classification. Therefore, we propose an embarrassingly simple but effective method that decouples the standard classifier into two heads. Then, these two individual heads are capable of independently addressing clear positive samples and noisy negative samples which are caused by the missing label. In this way, the model can effectively learn novel classes while mitigating the effects of noisy negative samples. Without bells and whistles, our model without any additional computation cost and parameters consistently outperforms its baseline and state-of-the-art by a large margin on PASCAL VOC and MS-COCO benchmarks for FSOD and FSIS tasks. The Code is available at https://csgaobb.github.io/Projects/DCFS.

Image Segmentation via Variational Model Based Tailored UNet: A Deep Variational Framework

Traditional image segmentation methods, such as variational models based on partial differential equations (PDEs), offer strong mathematical interpretability and precise boundary modeling, but often suffer from sensitivity to parameter settings and high computational costs. In contrast, deep learning models such as UNet, which are relatively lightweight in parameters, excel in automatic feature extraction but lack theoretical interpretability and require extensive labeled data. To harness the complementary strengths of both paradigms, we propose Variational Model Based Tailored UNet (VM_TUNet), a novel hybrid framework that integrates the fourth-order modified Cahn-Hilliard equation with the deep learning backbone of UNet, which combines the interpretability and edge-preserving properties of variational methods with the adaptive feature learning of neural networks. Specifically, a data-driven operator is introduced to replace manual parameter tuning, and we incorporate the tailored finite point method (TFPM) to enforce high-precision boundary preservation. Experimental results on benchmark datasets demonstrate that VM_TUNet achieves superior segmentation performance compared to existing approaches, especially for fine boundary delineation.

Distributed Nonparametric Estimation: from Sparse to Dense Samples per Terminal

Consider the communication-constrained problem of nonparametric function estimation, in which each distributed terminal holds multiple i.i.d. samples. Under certain regularity assumptions, we characterize the minimax optimal rates for all regimes, and identify phase transitions of the optimal rates as the samples per terminal vary from sparse to dense. This fully solves the problem left open by previous works, whose scopes are limited to regimes with either dense samples or a single sample per terminal. To achieve the optimal rates, we design a layered estimation protocol by exploiting protocols for the parametric density estimation problem. We show the optimality of the protocol using information-theoretic methods and strong data processing inequalities, and incorporating the classic balls and bins model. The optimal rates are immediate for various special cases such as density estimation, Gaussian, binary, Poisson and heteroskedastic regression models.

Computing Approximate Graph Edit Distance via Optimal Transport

Given a graph pair $(G^1, G^2)$, graph edit distance (GED) is defined as the minimum number of edit operations converting $G^1$ to $G^2$. GED is a fundamental operation widely used in many applications, but its exact computation is NP-hard, so the approximation of GED has gained a lot of attention. Data-driven learning-based methods have been found to provide superior results compared to classical approximate algorithms, but they directly fit the coupling relationship between a pair of vertices from their vertex features. We argue that while pairwise vertex features can capture the coupling cost (discrepancy) of a pair of vertices, the vertex coupling matrix should be derived from the vertex-pair cost matrix through a more well-established method that is aware of the global context of the graph pair, such as optimal transport. In this paper, we propose an ensemble approach that integrates a supervised learning-based method and an unsupervised method, both based on optimal transport. Our learning method, GEDIOT, is based on inverse optimal transport that leverages a learnable Sinkhorn algorithm to generate the coupling matrix. Our unsupervised method, GEDGW, models GED computation as a linear combination of optimal transport and its variant, Gromov-Wasserstein discrepancy, for node and edge operations, respectively, which can be solved efficiently without needing the ground truth. Our ensemble method, GEDHOT, combines GEDIOT and GEDGW to further boost the performance. Extensive experiments demonstrate that our methods significantly outperform the existing methods in terms of the performance of GED computation, edit path generation, and model generalizability.

A Simplified Algorithm for Joint Real-Time Synchronization, NLoS Identification, and Multi-Agent Localization

Real-time, high-precision localization in large-scale wireless networks faces two primary challenges: clock offsets caused by network asynchrony and non-line-of-sight (NLoS) conditions. To tackle these challenges, we propose a low-complexity real-time algorithm for joint synchronization and NLoS identification-based localization. For precise synchronization, we resolve clock offsets based on accumulated time-of-arrival measurements from all the past time instances, modeling it as a large-scale linear least squares (LLS) problem. To alleviate the high computational burden of solving this LLS, we introduce the blockwise recursive Moore-Penrose inverse (BRMP) technique, a generalized recursive least squares approach, and derive a simplified formulation of BRMP tailored specifically for the real-time synchronization problem. Furthermore, we formulate joint NLoS identification and localization as a robust least squares regression (RLSR) problem and address it by using an efficient iterative approach. Simulations show that the proposed algorithm achieves sub-nanosecond synchronization accuracy and centimeter-level localization precision, while maintaining low computational overhead.

Convergence analysis of wide shallow neural operators within the framework of Neural Tangent Kernel

Neural operators are aiming at approximating operators mapping between Banach spaces of functions, achieving much success in the field of scientific computing. Compared to certain deep learning-based solvers, such as Physics-Informed Neural Networks (PINNs), Deep Ritz Method (DRM), neural operators can solve a class of Partial Differential Equations (PDEs). Although much work has been done to analyze the approximation and generalization error of neural operators, there is still a lack of analysis on their training error. In this work, we conduct the convergence analysis of gradient descent for the wide shallow neural operators within the framework of Neural Tangent Kernel (NTK). The core idea lies on the fact that over-parameterization and random initialization together ensure that each weight vector remains near its initialization throughout all iterations, yielding the linear convergence of gradient descent. In this work, we demonstrate that under the setting of over-parametrization, gradient descent can find the global minimum regardless of whether it is in continuous time or discrete time.