An Efficient and Adaptive Granular-ball Generation Method in Classification Problem

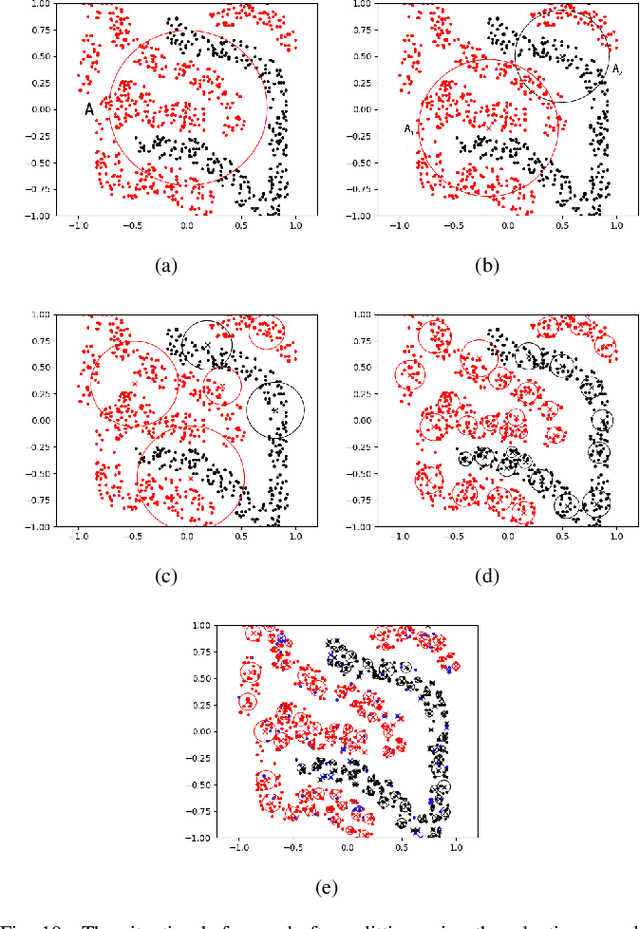
Granular-ball computing is an efficient, robust, and scalable learning method for granular computing. The basis of granular-ball computing is the granular-ball generation method. This paper proposes a method for accelerating the granular-ball generation using the division to replace $k$-means. It can greatly improve the efficiency of granular-ball generation while ensuring the accuracy similar to the existing method. Besides, a new adaptive method for the granular-ball generation is proposed by considering granular-ball's overlap eliminating and some other factors. This makes the granular-ball generation process of parameter-free and completely adaptive in the true sense. In addition, this paper first provides the mathematical models for the granular-ball covering. The experimental results on some real data sets demonstrate that the proposed two granular-ball generation methods have similar accuracies with the existing method while adaptiveness or acceleration is realized.

An Efficient and Accurate Rough Set for Feature Selection, Classification and Knowledge Representation

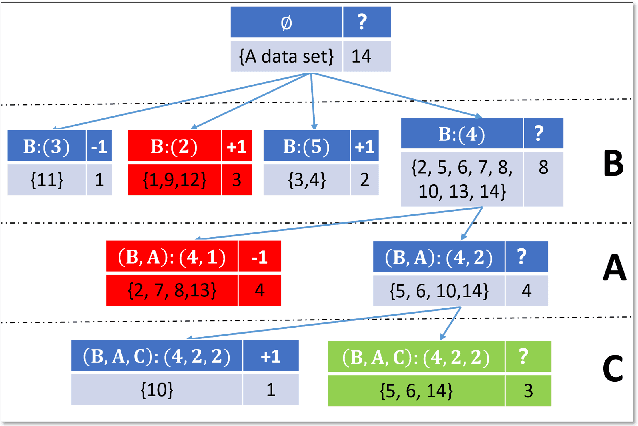
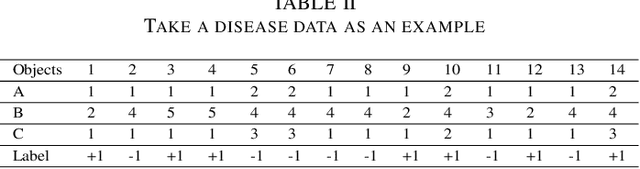
This paper present a strong data mining method based on rough set, which can realize feature selection, classification and knowledge representation at the same time. Rough set has good interpretability, and is a popular method for feature selections. But low efficiency and low accuracy are its main drawbacks that limits its application ability. In this paper,corresponding to the accuracy, we first find the ineffectiveness of rough set because of overfitting, especially in processing noise attribute, and propose a robust measurement for an attribute, called relative importance.we proposed the concept of "rough concept tree" for knowledge representation and classification. Experimental results on public benchmark data sets show that the proposed framework achieves higher accurcy than seven popular or the state-of-the-art feature selection methods.

GBRS: An Unified Model of Pawlak Rough Set and Neighborhood Rough Set

Pawlak rough set and neighborhood rough set are the two most common rough set theoretical models. Pawlawk can use equivalence classes to represent knowledge, but it cannot process continuous data; neighborhood rough sets can process continuous data, but it loses the ability of using equivalence classes to represent knowledge. To this end, this paper presents a granular-ball rough set based on the granlar-ball computing. The granular-ball rough set can simultaneously represent Pawlak rough sets, and the neighborhood rough set, so as to realize the unified representation of the two. This makes the granular-ball rough set not only can deal with continuous data, but also can use equivalence classes for knowledge representation. In addition, we propose an implementation algorithms of granular-ball rough sets. The experimental resuts on benchmark datasets demonstrate that, due to the combination of the robustness and adaptability of the granular-ball computing, the learning accuracy of the granular-ball rough set has been greatly improved compared with the Pawlak rough set and the traditional neighborhood rough set. The granular-ball rough set also outperforms nine popular or the state-of-the-art feature selection methods.

LRA: an accelerated rough set framework based on local redundancy of attribute for feature selection

In this paper, we propose and prove the theorem regarding the stability of attributes in a decision system. Based on the theorem, we propose the LRA framework for accelerating rough set algorithms. It is a general-purpose framework which can be applied to almost all rough set methods significantly . Theoretical analysis guarantees high efficiency. Note that the enhancement of efficiency will not lead to any decrease of the classification accuracy. Besides, we provide a simpler prove for the positive approximation acceleration framework.