An Efficient and Adaptive Granular-ball Generation Method in Classification Problem
Paper and Code
Jan 12, 2022
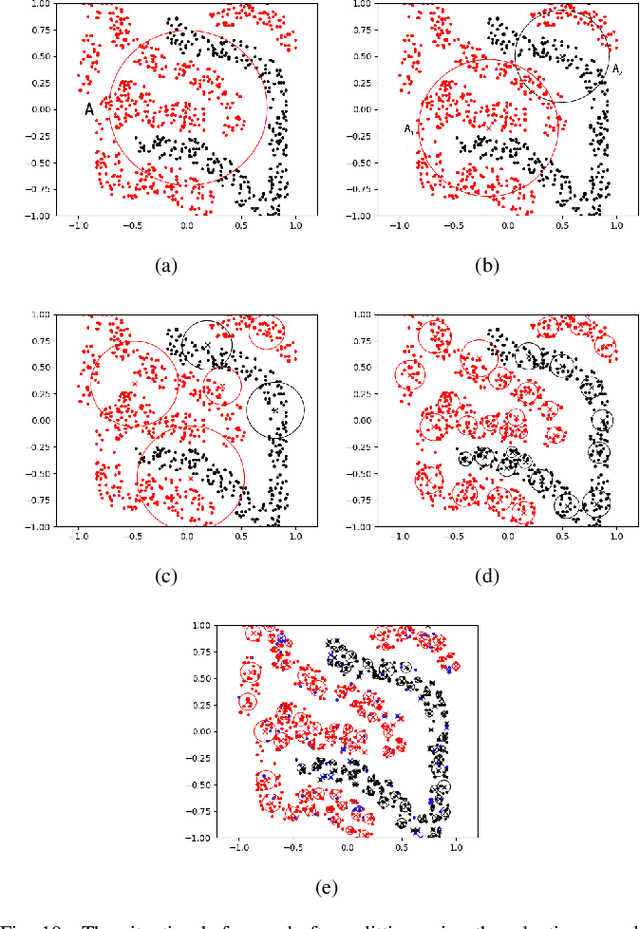


Granular-ball computing is an efficient, robust, and scalable learning method for granular computing. The basis of granular-ball computing is the granular-ball generation method. This paper proposes a method for accelerating the granular-ball generation using the division to replace $k$-means. It can greatly improve the efficiency of granular-ball generation while ensuring the accuracy similar to the existing method. Besides, a new adaptive method for the granular-ball generation is proposed by considering granular-ball's overlap eliminating and some other factors. This makes the granular-ball generation process of parameter-free and completely adaptive in the true sense. In addition, this paper first provides the mathematical models for the granular-ball covering. The experimental results on some real data sets demonstrate that the proposed two granular-ball generation methods have similar accuracies with the existing method while adaptiveness or acceleration is realized.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge