Static Batching of Irregular Workloads on GPUs: Framework and Application to Efficient MoE Model Inference

It has long been a problem to arrange and execute irregular workloads on massively parallel devices. We propose a general framework for statically batching irregular workloads into a single kernel with a runtime task mapping mechanism on GPUs. We further apply this framework to Mixture-of-Experts (MoE) model inference and implement an optimized and efficient CUDA kernel. Our MoE kernel achieves up to 91% of the peak Tensor Core throughput on NVIDIA H800 GPU and 95% on NVIDIA H20 GPU.

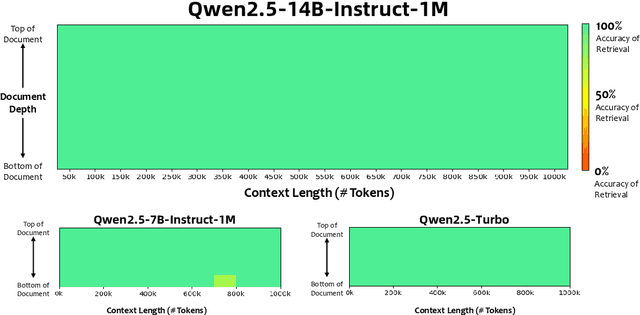
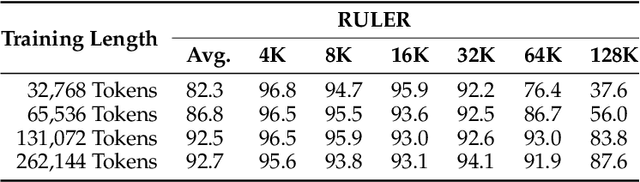
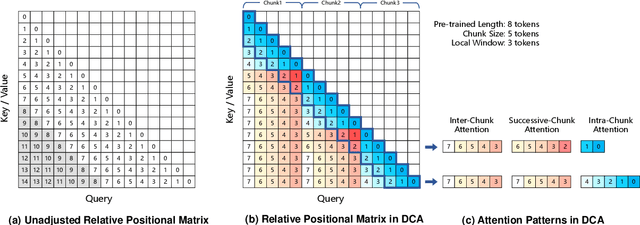
Qwen2.5-1M Technical Report

We introduce Qwen2.5-1M, a series of models that extend the context length to 1 million tokens. Compared to the previous 128K version, the Qwen2.5-1M series have significantly enhanced long-context capabilities through long-context pre-training and post-training. Key techniques such as long data synthesis, progressive pre-training, and multi-stage supervised fine-tuning are employed to effectively enhance long-context performance while reducing training costs. To promote the use of long-context models among a broader user base, we present and open-source our inference framework. This framework includes a length extrapolation method that can expand the model context lengths by at least four times, or even more, without additional training. To reduce inference costs, we implement a sparse attention method along with chunked prefill optimization for deployment scenarios and a sparsity refinement method to improve precision. Additionally, we detail our optimizations in the inference engine, including kernel optimization, pipeline parallelism, and scheduling optimization, which significantly enhance overall inference performance. By leveraging our inference framework, the Qwen2.5-1M models achieve a remarkable 3x to 7x prefill speedup in scenarios with 1 million tokens of context. This framework provides an efficient and powerful solution for developing applications that require long-context processing using open-source models. The Qwen2.5-1M series currently includes the open-source models Qwen2.5-7B-Instruct-1M and Qwen2.5-14B-Instruct-1M, as well as the API-accessed model Qwen2.5-Turbo. Evaluations show that Qwen2.5-1M models have been greatly improved in long-context tasks without compromising performance in short-context scenarios. Specifically, the Qwen2.5-14B-Instruct-1M model significantly outperforms GPT-4o-mini in long-context tasks and supports contexts eight times longer.

Exact Acceleration of Subgraph Graph Neural Networks by Eliminating Computation Redundancy

Graph neural networks (GNNs) have become a prevalent framework for graph tasks. Many recent studies have proposed the use of graph convolution methods over the numerous subgraphs of each graph, a concept known as subgraph graph neural networks (subgraph GNNs), to enhance GNNs' ability to distinguish non-isomorphic graphs. To maximize the expressiveness, subgraph GNNs often require each subgraph to have equal size to the original graph. Despite their impressive performance, subgraph GNNs face challenges due to the vast number and large size of subgraphs which lead to a surge in training data, resulting in both storage and computational inefficiencies. In response to this problem, this paper introduces Ego-Nets-Fit-All (ENFA), a model that uniformly takes the smaller ego nets as subgraphs, thereby providing greater storage and computational efficiency, while at the same time guarantees identical outputs to the original subgraph GNNs even taking the whole graph as subgraphs. The key is to identify and eliminate the redundant computation among subgraphs. For example, a node $v_i$ may appear in multiple subgraphs but is far away from all of their centers (the unsymmetric part between subgraphs). Therefore, its first few rounds of message passing within each subgraph can be computed once in the original graph instead of being computed multiple times within each subgraph. Such strategy enables our ENFA to accelerate subgraph GNNs in an exact way, unlike previous sampling approaches that often lose the performance. Extensive experiments across various datasets reveal that compared with the conventional subgraph GNNs, ENFA can reduce storage space by 29.0% to 84.5% and improve training efficiency by up to 1.66x.

AsymKV: Enabling 1-Bit Quantization of KV Cache with Layer-Wise Asymmetric Quantization Configurations

Large language models have shown exceptional capabilities in a wide range of tasks, such as text generation and video generation, among others. However, due to their massive parameter count, these models often require substantial storage space, imposing significant constraints on the machines deploying LLMs. To overcome this limitation, one research direction proposes to compress the models using integer replacements for floating-point numbers, in a process known as Quantization. Some recent studies suggest quantizing the key and value cache (KV Cache) of LLMs, and designing quantization techniques that treat the key and value matrices equivalently. This work delves deeper into the asymmetric structural roles of KV Cache, a phenomenon where the transformer's output loss is more sensitive to the quantization of key matrices. We conduct a systematic examination of the attention output error resulting from key and value quantization. The phenomenon inspires us to propose an asymmetric quantization strategy. Our approach allows for 1-bit quantization of the KV cache by implementing distinct configurations for key and value matrices. We carry out experiments across a variety of datasets, demonstrating that our proposed model allows for the quantization of up to 75% decoder layers with 1 bit, while simultaneously maintaining performance levels comparable to those of the models with floating parameters.

Unicron: Economizing Self-Healing LLM Training at Scale

Training large-scale language models is increasingly critical in various domains, but it is hindered by frequent failures, leading to significant time and economic costs. Current failure recovery methods in cloud-based settings inadequately address the diverse and complex scenarios that arise, focusing narrowly on erasing downtime for individual tasks without considering the overall cost impact on a cluster. We introduce Unicron, a workload manager designed for efficient self-healing in large-scale language model training. Unicron optimizes the training process by minimizing failure-related costs across multiple concurrent tasks within a cluster. Its key features include in-band error detection for real-time error identification without extra overhead, a dynamic cost-aware plan generation mechanism for optimal reconfiguration, and an efficient transition strategy to reduce downtime during state changes. Deployed on a 128-GPU distributed cluster, Unicron demonstrates up to a 1.9x improvement in training efficiency over state-of-the-art methods, significantly reducing failure recovery costs and enhancing the reliability of large-scale language model training.

LON-GNN: Spectral GNNs with Learnable Orthonormal Basis

In recent years, a plethora of spectral graph neural networks (GNN) methods have utilized polynomial basis with learnable coefficients to achieve top-tier performances on many node-level tasks. Although various kinds of polynomial bases have been explored, each such method adopts a fixed polynomial basis which might not be the optimal choice for the given graph. Besides, we identify the so-called over-passing issue of these methods and show that it is somewhat rooted in their less-principled regularization strategy and unnormalized basis. In this paper, we make the first attempts to address these two issues. Leveraging Jacobi polynomials, we design a novel spectral GNN, LON-GNN, with Learnable OrthoNormal bases and prove that regularizing coefficients becomes equivalent to regularizing the norm of learned filter function now. We conduct extensive experiments on diverse graph datasets to evaluate the fitting and generalization capability of LON-GNN, where the results imply its superiority.